マンデルブロ集合
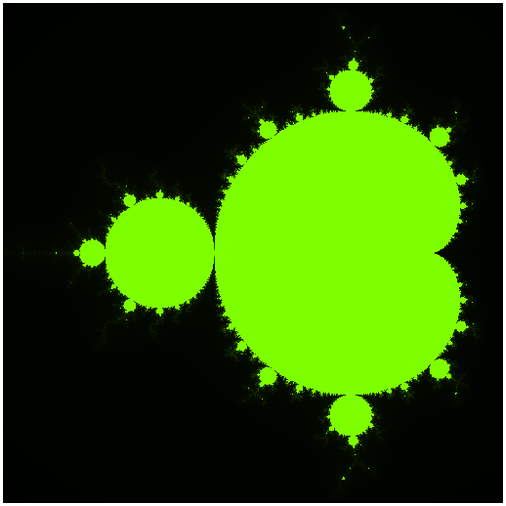
今回のサンプルの実行結果
マンデルブロとは
前回は、GLSL を用いて様々な図形をレンダリングすることに挑戦してみました。
単純な光の輪のレンダリングに始まり、最終的には花模様や風車のような不思議な図形をレンダリングすることができましたね。
続く今回は、フラクタル図形として非常に有名な、あのマンデルブロ集合をレンダリングしてみたいと思います。
マンデルブロ集合は、この集合の名前にもなっているマンデルブロ氏によって提唱されたもので、非常に複雑で、かつ美しい図形を描画できることから、プログラミングの世界では比較的有名です。近年では、一般に普及しているマシンでも高速な処理が可能となってきましたので、マンデルブロ集合のような複雑な計算が必要な幾何学模様の出番もより増えてきているような気がします。
今回はあまり難しく考えなくてもいいように工夫してテキストを書いてみます。ちょっとだけ難しい話がでてくるかもしれませんが、粘り強く取り組んでみてください。
漸化式
数学には漸化式(ぜんかしき)と呼ばれる考え方があります。
正直に書いてしまうと、このテキストを書いている私自身、この漸化式という言葉を勉強したり見聞きしたりしたことはありませんでした。数学を専攻していたわけでもなかったですしね。しかし、厳密な意味での漸化式がどういうものなのかは、WebGL について解説する当サイトのテキストにおいてはあまり重要ではないでしょう。
しかし、まったく意味がわからないというのもどうにも気持ちが悪いですよね。
ざっくりと簡単に概念を理解するなら、漸化式とはある答えを導き出すためのルールを表現した数式のことだと考えるのがいいと思います。
つまり、マンデルブロ集合という答えを導き出すためにはあるルールに則って計算を行う必要があります。そして、そのルールを記述した漸化式というものがあるわけですね。
ちなみに、マンデルブロ集合の漸化式は以下のような感じになっています。
マンデルブロ集合の漸化式
Zn+1 = Zn2 + C
なおかつ
Z0 = 0
はい、よくわかりませんね。
しかしここでめげてはいけません。
大丈夫です、きっと理解できます。
漸化式は、先ほども書いたとおり、ある答えを導き出すためのルールを記述したものでしかありません。そして、上記の漸化式の Z0 の場合をスタート地点として、再帰的にどんどん計算を繰り返していきます。
ここでは仮に、C には単純に 1 という数字を入れてみましょう。
C = 1 として n = 0 から n = 3 まで
漸化式
Zn+1 = Zn2 + C
Z0 = 0
漸化式を元に繰り返し計算する
Z0 = 0
Z1 = 02 + 1 = 1
Z2 = 12 + 1 = 2
Z3 = 22 + 1 = 5
どうでしょう。漸化式を元に計算してみると n の値が増えるほどに、どんどん数字が大きくなっているのがわかると思います。このまま n が無限に大きくなっていくとすると、答えも当然無限大に大きくなっていってしまいます。
この、無限に大きくなっていってしまう状態のことを発散すると表現します。これはなんとなく、イメージしやすいですね。
では続いて、漸化式における C が -1 だった場合にはどうなるのか考えてみましょう。
C = -1 として n = 0 から n = 3 まで
漸化式
Zn+1 = Zn2 + C
Z0 = 0
漸化式を元に繰り返し計算する
Z0 = 0
Z1 = 02 + (-1) = -1
Z2 = (-1)2 + (-1) = 0
Z3 = 02 + (-1) = -1
はい、このようになります。
先ほどと同じ漸化式で計算しているのに、C に -1 を入れた場合では数字が一向に増えていきません。むしろ、-1 と 0 との間を繰り返し行き来しています。
このように、一定の範囲を行き来する状態を振動すると表現します。これも、なんとなく言葉の意味をそのままイメージできますね。
このように、漸化式の C にどんな値が入ったかによって、発散するものと振動するものが出てきます。これこそが実はマンデルブロ集合を理解するためのキーポイントなのです。
マンデルブロ集合とシェーダ
実はマンデルブロ集合とは、その名前からもわかるとおりなにかの集合です。なにかが、集合している様子のことを指しているわけです。
じゃあ、いったいなにが集合していることを言うのでしょうか。実は、先ほどの漸化式で振動状態になる部分の集合のことを、マンデルブロ集合というのです。
本テキストの冒頭に出てきているサンプルの実行結果を見ると、色が付いている部分と、真っ黒な部分とがありますよね。実はこのなかで一番明るい色が付いている部分、これがマンデルブロ集合です。
ちょっとわかりにくいと思うので別の画像で見てみます。
マンデルブロ集合の拡大図


拡大図を見ると、真っ白な部分とそうでない部分があると思います。マンデルブロ集合とは、上の画像で言うと白い部分のことを言います。
先ほどの画像は、シェーダでマンデルブロ集合の漸化式を計算し、発散するまでにかかった回数をもとにして色づけしています。先述のとおり、マンデルブロ集合とは漸化式によって発散しない、振動状態となる部分の集合です。つまり、白い部分は最後まで値が発散しなった部分なんですね。
逆に、グレーになっている部分や黒になっている部分は、漸化式を計算しているうちに値が発散してしまった部分です。この発散までにかかった回数を指標として色にして出力したのが、先ほどの画像というわけです。
それでは、実際にどのようなシェーダのコードになっているのか見てみましょう。
マンデルブロ集合シェーダ
precision mediump float;
uniform float time;
uniform vec2 mouse;
uniform vec2 resolution;
// HSV カラー生成関数
vec3 hsv(float h, float s, float v){
vec4 t = vec4(1.0, 2.0 / 3.0, 1.0 / 3.0, 3.0);
vec3 p = abs(fract(vec3(h) + t.xyz) * 6.0 - vec3(t.w));
return v * mix(vec3(t.x), clamp(p - vec3(t.x), 0.0, 1.0), s);
}
void main(void){
// マウス座標の正規化
vec2 m = vec2(mouse.x * 2.0 - 1.0, -mouse.y * 2.0 + 1.0);
// フラグメント座標の正規化
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, resolution.y);
// マンデルブロ集合
int j = 0; // カウンタ
vec2 x = p + vec2(-0.5, 0.0); // 原点を少しずらす
float y = 1.5 - mouse.x * 0.5; // マウス座標を使って拡大度を変更
vec2 z = vec2(0.0, 0.0); // 漸化式 Z の初期値
// 漸化式の繰り返し処理(今回は 360 回ループ)
for(int i = 0; i < 360; i++){
j++;
if(length(z) > 2.0){break;}
z = vec2(z.x * z.x - z.y * z.y, 2.0 * z.x * z.y) + x * y;
}
// 時間の経過で色を HSV 出力する
float h = mod(time * 20.0, 360.0) / 360.0;
vec3 rgb = hsv(h, 1.0, 1.0);
// 漸化式で繰り返した回数をもとに輝度を決める
float t = float(j) / 360.0;
// 最終的な色の出力
gl_FragColor = vec4(rgb * t, 1.0);
}前回までとは異なり、ちょっと複雑ですね。
ここはひとつ焦らず、最初から見ていきましょう。
まず冒頭では、いつも通りの uniform 変数が登場し、その下に HSV で色を指定できる関数をシェーダ内に定義しています。これの中身については解説しませんが、HSV のそれぞれを 0 ~ 1 の範囲に正規化して渡すことで RGB に変換して返してくれます。※この関数は色づけに非常に便利なので今後も時折使うと思います。
続いて前回までのサンプルと同じように、マウス座標や処理の対象となるフラグメント座標の正規化が入ります。これはまったく同じなので説明不要でしょう。
そしてその下からがマンデルブロ集合のためのコード群です。
必要な変数を初期化する
// マンデルブロ集合
int j = 0; // カウンタ
vec2 x = p + vec2(-0.5, 0.0); // 原点を少しずらす
float y = 1.5 - mouse.x * 0.5; // マウス座標を使って拡大度を変更
vec2 z = vec2(0.0, 0.0); // 漸化式 Z の初期値まず初期化の段階では四つの変数を定義します。
ここは紛らわしいと思いますが、型の違いなどに注意しつつ見ていきましょう。
まず変数 j は単純にカウンタとして使います。先ほども少し触れましたが、今回のサンプルでは発散までに要した繰り返しの回数をもとに色づけします。これをループの外でも参照できるようにするためにここで初期化しておきます。
続いて変数 x ですが、こちらは vec2 型ですね。マンデルブロ集合を描く位置を少しずらすためにこの変数は使います。つまり、この部分を変更すると、最終的にスクリーン上に描かれるマンデルブロ集合全体の位置が移動します。
また、マウスの挙動によって拡大率を変化させるために変数 y を使います。
変数 z は漸化式の Z です。初期値は 0 である必要がありますので、ループが始まる前に初期化しておきます。
ループで漸化式を処理する
// 漸化式の繰り返し処理(今回は 360 回ループ)
for(int i = 0; i < 360; i++){
j++;
if(length(z) > 2.0){break;}
z = vec2(z.x * z.x - z.y * z.y, 2.0 * z.x * z.y) + x * y;
}続いては漸化式のループです。
先ほどは Z0 から Z3 まででどんな結果になるかを例に挙げました。実際のシェーダでは、贅沢に Z360 まで計算してみましょう。当然、このループの回数を増やすことでより正確なマンデルブロ集合を描くことができますが、それに伴い動作も重くなります。
ループのなかでは、カウンタをインクリメントした後、Z の値(この場合長さですね)が 2.0 を超えていないかチェックしています。もし、値が 2.0 を上回っている場合、その点は確実に発散します。つまり、ループ処理中にここではじかれた地点は、確実にマンデルブロ集合には属さないと判断できます。
ちょっと整理しましょう。
漸化式を繰り返し処理していくなかで、値が発散したかどうかは length(z) が 2.0 を上回ったかどうかで判断できます。
その時点までに何度ループしたかは、カウンタである変数 j に入っていますよね。
ループ処理を抜けるのが早ければ早いほど、カウンタの値は小さいはずです。また逆に、カウンタの値が大きいということは、長い時間ループしたか、もしくは最後まで値が発散しなかったかのいずれかということになります。
カウンタをもとに色づけ
// 時間の経過で色を HSV 出力する
float h = mod(time * 20.0, 360.0) / 360.0;
vec3 rgb = hsv(h, 1.0, 1.0);
// 漸化式で繰り返した回数をもとに輝度を決める
float t = float(j) / 360.0;
// 最終的な色の出力
gl_FragColor = vec4(rgb * t, 1.0);ここで注目すべきは変数 j を使って輝度を求めている部分です。
ループの最大回数は 360 回でしたよね。ですから、カウンタの値を 360 で割って正規化してやると、その値はおのずと 0 ~ 1 の範囲に定まります。最後まで発散しなかった場所ほど、数値が大きくなるという寸法ですね。
マンデルブロ集合の周はすべてつながっている
マンデルブロ集合は拡大することで次々と美しい模様が見えてきます。マンデルブロ集合本体と、その外側との境界部分には、色付けなどを工夫することで実に美しい模様が浮かび上がります。しかし、実に不思議なことですが、それら境界線の全てはひとつの線としてつながっており、途切れてしまう場所はどこまで拡大しても永遠に出てはこないそうです。
これはすなわち、マンデルブロ集合と同じ形をした風船が仮にあったとすると、その中に空気をいくら詰めても、どこからも空気が漏れることはないということでもあります。また、一見すると穴が開いているように見える場所であっても、実際に穴が開いているわけではなく非常に細かなひとつの線として繋がっています。
理屈の上では、マンデルブロ集合はどこまででも拡大できます。しかしどれだけ拡大しても、境界線の部分が途切れてしまうところは永遠に出てこない……つまり、その周は無限大なのです。なんだかすごく不思議ですね。
まとめ
さて、マンデルブロ集合について見てきましたが、いかがでしたか。
若干数学的に難しそうな単語が出てきたりしましたが、ざっくりと、マンデルブロ集合とはなんなのか、またどのような仕組みで描かれるのかは理解できたのではないでしょうか。
シェーダ内では、パラメータ的要素を持つ値をいくつか使っています。描画される位置をずらしてみたり、あるいはより拡大して表示してみたり、値を少し変えるだけで様々に描画結果が変化するでしょう。自分なりに改造してみると、いろいろ発見できると思います。
サンプルはいつものように以下のリンクから。
