深度値と座標系について理解する

深度値との長い闘いの幕開け

さて、前回まではサンプルを紹介することが多かったですが、今回は「深度値」についてあらためて考えてみたいと思います。

ご存じのとおり、デプスシャドウなどと呼ばれる深度値を用いた影の表現には、一度フレームバッファに深度を描き込み最終的にそれをテクスチャから読み出して再利用するという手順があります。この「描き込み」 → 「読み出し」の部分をしっかり行わないと、深度値を正しく橋渡しすることができません。

WebGL には、本家 OpenGL や DirectX などのような最初から備わっている便利機能が実装されていないことが多く、今回の場合も自前でいろいろとやる必要があります。また、それには少なからず深度というものに関する予備知識が必要なように思います。今回は、この深度値の取り扱いについてあらためて解説したいと思います。

このテキストの執筆には @hiyoko1986 さんに多数の助言を頂きました。ありがとうございます。

そもそも深度値とは

さて、それでは早速ですが深度値についてひとつひとつ紐解いていきましょう。

まず唐突ですが、深度値とはそもそもなんなのでしょうか。場合によっては Z 値などと言ったりもしますね。これは、現実世界で当り前のように起こっている「手前に不透明な物体があったらその向こう側は見えなくなる」などの現象を再現するために 3D プログラミングには欠かせない概念です。

深度値を格納している専用のバッファである「深度バッファ」には、初期化された際はもちろんのこと、なにかしらのモデルがレンダリングされるたびに 0 ～ 1 の範囲の数値が描き込まれていきます。特殊なことをせずモデルを普通にスクリーン上にレンダリングするだけであれば、この深度値や深度バッファについて深く考えていなくても、勝手に WebGL が深度値をうまいこと使って処理を行ってくれます。

しかし、デプスシャドウを行う場合や、その他深度値を使って特殊なことをやりたいとなった場合には話が変わってきます。なんとかして、この深度バッファが持っている情報を使いたいという場面に出くわすわけです。しかし残念ながら、深度バッファの値を直接読み出すことはできません。深度バッファがやっていることと同様のことを、プログラム側で自前でやってやる必要があります。

ローカル座標系

深度値を自前で処理するといっても、具体的にはなにをいったいどうすればいいのでしょうか。

深度バッファの値が直接読み出せないのであれば、深度値をテクスチャに値として格納しておき、このテクスチャをあとで参照することで深度を読み出せばいいですね。テクスチャに一度格納するタイミングと、テクスチャから深度を読み出すタイミング、この二か所を正しく処理することができれば、深度値をシェーダ内で利用することができます。

ここで問題になるのは、テクスチャに何を描き込むのかです。

頂点シェーダに送られてくる attribute 変数の頂点位置をそのまま単純に描き込んでも、それではまるで意味がないことは最低限わかると思います。ここでいう attribute 変数の頂点位置はローカル座標系だからです。

はい、出ました。座標系というこのキーワード。

いまだに自分もそうですが、この「座標系」という言葉が出てくると途端に話が難しくなったような気がしますね。でも今回のテキストはわかりやすさ重視で書いていきます。ですから安心して読み進めていただければと思います。

ローカル座標系とは、簡単に言うと「モデリングソフトが出力したそのまんまの頂点位置」です。もちろん、当サイトのサンプルでもたびたび登場しているような、自前で球体やトーラスを用意している場合でも同様です。まだ一切加工されていない、モデルの持っている座標位置そのもの、それがローカル座標です。

普通、三次元空間上にモデルを配置する際、モデルを移動したり回転させたりといったことが行われます。ローカル座標は先ほども書いたようになんの加工もされていない素の状態です。座標変換行列でどんな移動や回転が掛けられる予定だとしても、ローカル座標はローカル座標、つまり行列を適用する前の状態ですから、これをテクスチャに描き込んでも無意味です。ここまでは簡単ですね。

同次座標系

ローカル座標系の次は、同次座標系です。

「だから難しい感じがするから座標系とか言うなよ！」と思うかもしれませんが、大丈夫です。簡単です。深度値を正しく扱うスキルを身につけるために、ちょっと回り道ですが同次座標についても理解しておきましょう。

同次座標系というのは、本来の次元数にプラス１次元した状態で計算を行うもの、というふうに考えるのが一番簡単だと思います。ちなみに、これは既に当サイトのサンプルでもさんざんやってきました。きっとこれをご覧のみなさんも既に使ったことがあるはずです。頂点シェーダの中にある一文を思い出してみましょう。

頂点シェーダ内でよく見るあの一文

gl_Position = mvpMatrix * vec4(position, 1.0)

はい、これは何度も見たことがありますね。むしろ当たり前のように毎回使っている処理です。ここで注目すべきは三次元として入ってきたローカル座標の頂点位置を vec4 によって四次元に変換して処理しているということです。

同次座標系では、先ほども書いたように次元がひとつ増えます。これにより、移動や回転といった柔軟な座標変換が可能になります。つまり三次元の頂点を行列を使って効率よく処理するために、同次座標系を使う大きなメリットがあるわけです。だから WebGL を始めとする 3D プログラミングの世界では 4 x 4 の行列を用いるのですね。

クリップ空間と正規化デバイス座標系

さて、深度値を正しく処理するための解説のはずが、なぜか座標系に関する解説が続いています。ちょっとうんざりするかもしれませんが、ここまではなんとなくでも理解できているでしょうか。

もう少しだけ、ちょっと小難しい話が続きますがゆっくりで構いませんので考えていきましょう。

先ほど登場した同次座標系のプラス１次元は、普通 W を用いて表されます。そしてこの四番目の要素 w は、3D 空間で視界よりも外側にあるかどうかの判断に実は使われています。

簡単に式にして表してみると次のような感じの規則で視界が決められています。

w を用いた視界のルール

 -w < x < w
 -w < y < w
 -w < z < w

そうなんです。実は w よりも大きい、あるいは -w よりも小さいという座標を持つ頂点は、視界に映らなくなってしまうのです。つまりレンダリングされません。

無限遠に広がる三次元空間上で、どの空間を切り取ってレンダリングすればいいのか、その鍵を握っているのが他ならぬ w の値なんですね。この w によってレンダリングされるべきと決められた空間は、空間を切り取っていることからクリップ空間などと呼ばれます。

そして、このクリップ空間の中にある頂点には w を使ったある計算が適用されます。その計算とは、X Y Z の各要素に対して w で除算する処理です。これを行うことにより、頂点の座標系は正規化デバイス座標系になります。

正規化デバイス座標系とは「正規化」の単語からもわかるように、すべての位置座標が正規化されて -1 ～ 1 の範囲に変換された座標系です。

だいぶややこしくなってきましたね。

以下のような例で考えてみましょう。

クリップ空間の模式図

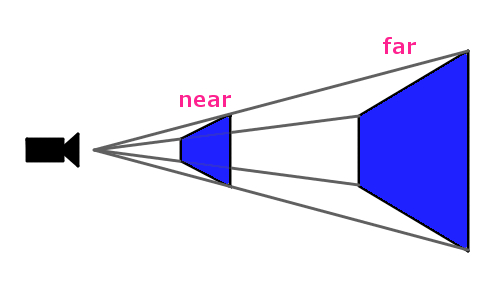
上記の near と far の間の部分がレンダリングされる予定の領域、つまりこれがクリップ空間です。

このクリップ空間の中にある頂点だけが実際にレンダリングされることになります。

そして、クリップ空間の中にある頂点には、先ほども説明したように X Y Z に対する w での除算が行われます。これにより、座標系が正規化デバイス座標系に変換されます。正規化デバイス座標系では、すべての座標は -1 ～ 1 の範囲に収まるように正規化されます。つまり、図式化すると以下のような状態になっているわけです。

正規化デバイス空間の模式図

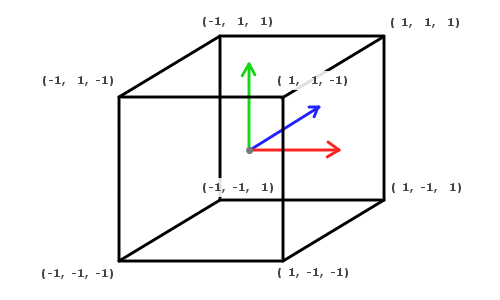
先ほどのクリップ空間の図では、クリップ空間は視錐台(しすいだい)状の形をしていましたね。前方クリップ面、つまり near の面は小さく、後方クリップ面である far の面は大きかったはずです。しかし、正規化デバイス空間では手前だろうと奥だろうと、すべてが正規化されているためクリップ空間は正六面体になっています。この正規化という行程を経ることによって、奥にあるものはより小さく、手前にあるものはより大きくなります。それによりあたかも遠近法と同じことが起こっているように見えるわけなんですね。

このような座標の正規化のためにも、同次座標系で登場した w は欠かせない存在なのですね。

やっと深度値の話

さて、正規化デバイス座標系までしっかり理解できたらいよいよ深度値の話ができます。だいぶ遠回りしました(笑)

先ほどから登場している正規化デバイス座標系は、正規化の名前からわかるとおり座標が一定の範囲内に必ず収まっています。これは、テクスチャに深度を描き込む際に非常に好都合ですね。

ご存じのとおり、テクスチャに描き込むことができるのは 0 ～ 1 までの範囲の値だけです。このことから gl_Position の値をそのまま描き込んでしまってはいけないということがわかります。たまたま同範囲内にある頂点の情報は描き込まれるかもしれませんが、範囲外にある値を持つ頂点がないとは限りません。というより、大抵はあるでしょう。

そこで、正規化デバイス座標系の出番です。

正規化デバイス座標系に座標系を変換するには、先ほどから書いているように w の値を使えばいいですね。三次元である頂点位置に対して w で割る処理を挟んでやることで、必ず頂点座標は -1 ～ 1 の範囲内に収まるようになります。しかしテクスチャに描き込める値は 0 ～ 1 の範囲ですから、正規化デバイス座標系のようにマイナスの値があると困ってしまいます。これには、1 足して 2 で割る処理をしてやればいいでしょう。

正規化デバイス座標系からさらに変換する

(vec3(x, y, z) / w + 1.0) / 2.0

このようにすると、-1 ～ 1 だったものが、0 ～ 1 になりますよね。

これをテクスチャに描き込んでやれば、正しく深度値を扱うことができるのです。いや～、長い旅路でしたが、紆余曲折を経て、頂点座標は正規化デバイス座標系へ変換することで、テクスチャに描き込むのに最適な状態になるというわけです。

しかしまだ終わらない深度の話

さて、深度値をテクスチャに描き込む方法については理解できましたか。

だいぶ余計な知識をフル活用しなければならなかったので、もしかすると一度や二度では読んでも理解できないかもしれませんが、根気強く取り組んでいただければと思います。

そして、ここからはオマケのようなものですが、深度値を用いる代表的な処理の一つ、シャドウマッピングを例にとりつつ深度値を扱う際の注意点にも触れておきます。

当サイトにあるシャドウマッピングのサンプルは、上記で長々と解説したような正しい深度値の扱いでの実装になっていません。正直に書きますが、これは該当テキストの執筆当時の私自身が、ちゃんと正しく理解することができていなかったからです。

冒頭にも書いたように @hiyoko1986 さんが指摘してくれたことがきっかけとなり、あらためて勉強しなおして本テキストを書きました。まだ間違ってるところがあるよ！ という方がいたらぜひ教えてください！

さて深度値について理解したところで、あらためて当サイトのシャドウマッピングのサンプルを修正していたのですが、深度値を扱う上ではもうひとつ大事なポイントがあったのです。それはクリップ空間の広さのです。

途中の解説でも書いたように、クリップ空間は最終的に正規化されることになるため、どれほど広大な空間も最後には -1 ～ 1 の範囲に収束します。これは言い換えると、クリッピング空間の余白の部分が広ければ広いほど、空間内は必要以上に正規化の影響を受けてしまうということでもあります。

これも、図式化してみるとわかりやすいでしょう。

余分なクリップ空間の余白

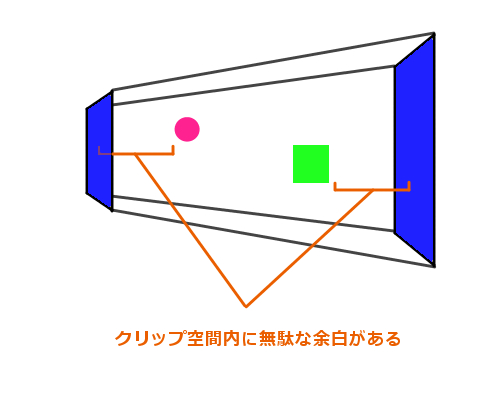
上のような状態では、一番近くにあるモデルと一番遠くにあるモデル、それぞれと前方クリップ面や後方クリップ面が離れています。最終的に座標が変換される際に、必要以上に無駄な拡大縮小効果が生まれてしまいます。これはすなわち、深度を計測する際に精度が著しく低下してしまうということでもあります。

一方、以下のような状態であれば、必要最低限の最適化しか行われなくなるため、高い精度を維持しやすくなります。

無駄のないクリップ空間

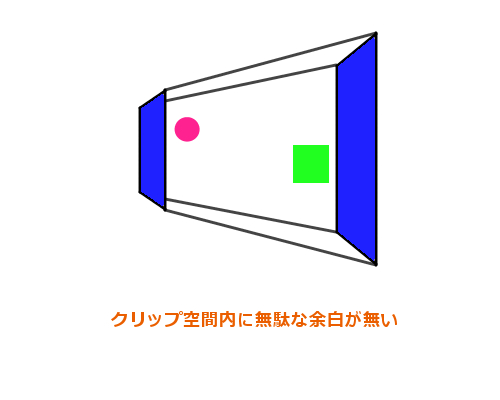
ある程度精度の高い深度値の判定が必要となるケースでは、無駄なくクリップ空間を設定することが重要です。いくら正確な深度をテクスチャに描き込んでも、それが必要以上の正規化をされた状態では肝心の精度が下がってしまいます。自分のプログラムを見返し、最低限のサイズのクリップ空間になるように気を配ってコーディングしましょう。

まとめ

さて、だいぶ文章ばかりの長いテキストになりましたが、いかがでしたでしょうか。

もともと自分自身があまり理解していない状態で、とりあえず動いてるから大丈夫だろうと甘く考えたことがいけなかったんですが、その間違いを指摘してくれる方がいらっしゃって、本当にありがたいと感じました。

自分自身がそうだったのでよくわかるのですが、座標系とか深度とか、あるいは行列とか。とにかく 3D には難解な部分がたくさんあります。今回のテキストも、わかりやすくは書いたつもりですが必ずしもすべての読者が理解できるかどうかと考えると、やっぱり難しいのかなと思います。

ただ、ひとつだけ確実なのは、あきらめずに何度も読み返したりウェブをあさったりすれば、いずれは必ず理解できるようになるということです。私のテキストがそのきっかけにでもなってくれていればいいなと思います。

さて、当テキストのサンプルは、上でも少し触れましたがシャドウマッピングのサンプルの改訂版です。

深度をテクスチャに描き込む部分、そして読み出した深度を比較する部分など、一部修正を加えてあります。深度値を描き込むシェーダでは、深度値を正規化して描き込むために以下のようになりました。

深度値格納用フラグメントシェーダ

precision mediump float;

varying vec4 vPosition;

void main(void){
	float depth = (vPosition.z / vPosition.w + 1.0) * 0.5;
	gl_FragColor = vec4(vec3(depth), 1.0);
}

頂点シェーダから入ってきた varying 変数 vPosition の Z 値に対して、第四の要素である W を用いた計算が適用されているのがわかると思います。

同様に、これをテクスチャから読み出したあと、その読み出した値と比較する数値の算出部分でも、以下のように正規化の行程を加えています。

シャドウマッピング用のフラグメントシェーダ

precision mediump float;

uniform mat4      invMatrix;
uniform vec3      lightPosition;
uniform sampler2D texture;
varying vec3      vPosition;
varying vec3      vNormal;
varying vec4      vColor;
varying vec4      vTexCoord;
varying vec4      vDepth;

void main(void){
	float lightCoord = 0.0;
	vec3  light     = lightPosition - vPosition;
	vec3  invLight  = normalize(invMatrix * vec4(light, 0.0)).xyz;
	float diffuse   = clamp(dot(vNormal, invLight), 0.2, 1.0);
	float shadow    = texture2DProj(texture, vTexCoord).r;
	vec4 depthColor = vec4(1.0);
	if(vDepth.w > 0.0){
		lightCoord = (vDepth.z / vDepth.w + 1.0) * 0.5;
		if((lightCoord - 0.01) > shadow){
			depthColor = vec4(0.5, 0.5, 0.5, 1.0);
		}
	}
	gl_FragColor = vColor * vec4(vec3(diffuse), 1.0) * depthColor;
}

ライトから見た場合の座標変換行列によって頂点を処理した結果が、上記の vDepth に入っています。先ほどの格納用シェーダと同様に、W の値を使って深度を正規化しているのがわかると思います。

これらの修正を加えたシャドウマッピングのサンプル改は、以下のリンクから実際に動作するものを見ることができます。

また、高解像度シャドウマップのサンプルも、併せて修正したものを用意しましたのでそちらも興味のある方は見てみるといいでしょう。

@h_doxas Twitter