クォータニオンと球面線形補間

今回のサンプルの実行結果
球面線形補間とは
前回はクォータニオンをモデル座標変換行列に適用し、マウス座標に応じて自由にモデルを回転させる方法を解説しました。
今回はクォータニオンを使って球面線形補間を行なってみます。クォータニオンによる球面線形補間では、あるクォータニオンから、別のクォータニオンへ、滑らかに補間された一意の姿勢を得ることができます。
わかりやすく言うと、球面線形補間を用いれば、ある回転を表すクォータニオン A から、別の回転を表すクォータニオン B の間を綺麗に補間した結果のうち、任意のタイミングでの状態を得ることが可能です。あんまりわかりやすくなってないか……あはは……
そもそも球面線形補間とはその名の通り、球面に沿って線形で補間できる補間方法のことです。クォータニオンを用いた球面線形補間では、二つのクォータニオンから補間結果を格納した新しいクォータニオンを生成することができます。
文章だけを読んでもなかなかイメージしにくいと思いますが、図を交えつつ、詳しく見ていきましょう。
まず、ものごとをわかりやすくするために、今回は X 軸を中心とした回転を行なうクォータニオン A と、Y 軸を中心とした回転を行なうクォータニオン B を考えてみます。
それぞれのクォータニオンによる回転を適用すると、モデルは次のように回転します。
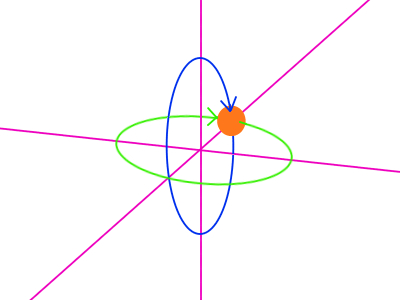
オレンジ色で表されているモデルは、Z 方向に少しずれた状態で三次元空間上に置かれています。このモデルに対して、原点を中心とした X 軸回転を与えたものが青い色で表されている軌道です。原点を中心とした Y 軸回転だと、緑色の軌道ですね。
この二つの回転から、球面線形補間を用いて補間後の軌道を表すと、例としては次のようになります。
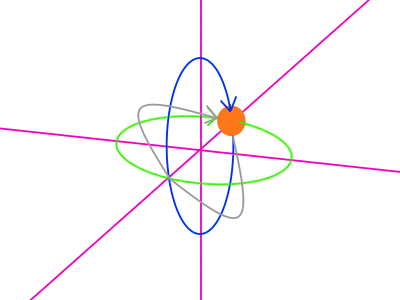
球面線形補間では、二つの回転の間を補間するときの時間値を設定できます。これは要するに、一方の回転から、もう一方の回転へ補間の比率とも考えることができます。時間値は 0 ~ 1 の範囲で設定し、時間値が 0.5 であれば、二つの回転のちょうど中間の補間結果を得ることができることを意味します。
時間値が 0 に近ければ近いほど、一つ目の回転に近い補間結果となります。逆に、1 に近づけば近づくほどに、二つ目の回転に近い補間結果となります。
球面線形補間についてざっくりと理解できたところで、実際の実装を見ていきます。
トーラスを球面線形補間で動かす
今回のサンプルでは、三つのモデルをレンダリングします。
一つ目のトーラスは原点を中心とした X 軸回転をするトーラス。二つ目は同様に Y 軸回転をするトーラスです。
三つ目のトーラスは、一つ目と二つ目の軌道を球面線形補間した起動で動くようにします。また、今回は時間値を任意に設定できるようにするために、HTML に range タイプの input タグを含めます。
シェーダは点光源を用いたフォンシェーディングで実装しますので、シェーダ周りは以前のものをそのまま使います。わかりにくい部分だけ、抜粋してコードを解説しましょう。
まず、先ほども書いた通り今回は input タグを使うので、javascript 内でこの input タグへの参照を取得しておきます。
range タイプ input タグへの参照を取得
// input range エレメント
var eRange = document.getElementById('range');input タグには id を付加しておき、上記のように javascript プログラムから参照できるようにしておきます。
レンダリングを行なう恒常ループの中では、三つのクォータニオンの処理を行ないます。
クォータニオンの生成と初期化自体は恒常ループの外側で行ないますが、そのクォータニオンに回転を与える処理や、二つのクォータニオンを球面線形補間する処理などは恒常ループのなかで行なう必要があります。
恒常ループの外側でクォータニオンを生成し初期化しておく
// 各種クォータニオンの生成と初期化
var q = new qtnIV();
var aQuaternion = q.identity(q.create());
var bQuaternion = q.identity(q.create());
var sQuaternion = q.identity(q.create());恒常ループ内でクォータニオンを操作する
// 恒常ループ
(function(){
// canvasを初期化
gl.clearColor(0.0, 0.0, 0.0, 1.0);
gl.clearDepth(1.0);
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
// カウンタをインクリメントしてラジアンを算出
count++;
var rad = (count % 360) * Math.PI / 180;
// 経過時間係数を算出
var time = eRange.value / 100;
// 回転クォータニオンの生成
q.rotate(rad, [1.0, 0.0, 0.0], aQuaternion);
q.rotate(rad, [0.0, 1.0, 0.0], bQuaternion);
q.slerp(aQuaternion, bQuaternion, time, sQuaternion);
// モデルのレンダリング
ambientColor = [0.5, 0.0, 0.0, 1.0];
draw(aQuaternion);
ambientColor = [0.0, 0.5, 0.0, 1.0];
draw(bQuaternion);
ambientColor = [0.0, 0.0, 0.5, 1.0];
draw(sQuaternion);
function draw(qtn){
// モデル座標変換行列の生成
q.toMatIV(qtn, qMatrix);
m.identity(mMatrix);
m.multiply(mMatrix, qMatrix, mMatrix);
m.translate(mMatrix, [0.0, 0.0, -5.0], mMatrix);
m.multiply(tmpMatrix, mMatrix, mvpMatrix);
m.inverse(mMatrix, invMatrix);
// uniform変数の登録と描画
gl.uniformMatrix4fv(uniLocation[0], false, mvpMatrix);
gl.uniformMatrix4fv(uniLocation[1], false, mMatrix);
gl.uniformMatrix4fv(uniLocation[2], false, invMatrix);
gl.uniform3fv(uniLocation[3], lightPosition);
gl.uniform3fv(uniLocation[4], camPosition);
gl.uniform4fv(uniLocation[5], ambientColor);
gl.drawElements(gl.TRIANGLES, torusData.i.length, gl.UNSIGNED_SHORT, 0);
}
// コンテキストの再描画
gl.flush();
// ループのために再帰呼び出し
setTimeout(arguments.callee, 1000 / 30);
})();今回はトーラスをレンダリングする部分の処理を関数化して、簡単に呼び出せるようにしてあります。
ここで登場する即席のレンダリング関数 draw は、引数にクォータニオンを受け取り、そのクォータニオンをモデル座標変換行列に適用した後、uniform 変数などを登録して描画します。
また、今回はどのトーラスがどの回転を適用されたものなのかわかりやすくするために、環境光の色を変更してからレンダリングしています。コードをよく見ればわかると思いますが、赤っぽい色でレンダリングされるトーラスは X 軸回転するトーラスです。同様に、緑っぽい色のトーラスが Y 軸回転するトーラス。そして、青っぽい色のトーラスが球面線形補間を行なった結果を反映するトーラスになります。
実際に球面線形補間を行なっているのは、当サイトのオリジナルライブラリである minMatrixb.js に実装されている qtnIV.slerp メソッドで、このメソッドは四つの引数を取ります。
第一引数には、球面線形補間の元となる一つ目のクォータニオン、第二引数は同様に二つ目のクォータニオンを指定します。第三引数が時間値で、これは 0 ~ 1 の範囲で指定するようにします。第四引数が補間後の回転を適用するクォータニオンになります。
HTML 内の input タグから取得した値を使って、時間値を設定しながら呼び出しているのがわかると思います。実際のサンプルを動作させてみれば、時間値を変更することによってどのような変化が起こるのか非常にわかりやすいと思います。
まとめ
クォータニオンによる球面線形補間では、二つの回転の間を滑らかに補間した、新しい回転を得ることが可能です。これは言葉だけで聞くとイマイチ意味がわかりにくいと思いますが、サンプルを動作させてみれば直感的に意味がわかると思います。
実際問題、この球面線形補間がどのような場面で役に立つのかはイメージしにくいかもしれませんが、時間値を設定しながら任意の補間結果が得られる球面線形補間は、応用力次第で様々な処理に力を発揮してくれるはずです。
次回はゲーム作成などの際に有用なテクニックとなる、ビルボードについてやろうと思っています。
