フラットシェーディング

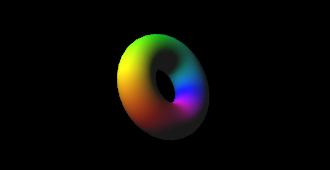
今回のサンプルの実行結果
あえて平坦に見せる
前回はカレントバッファの色情報を GPU から読み出し、CPU 側から参照することを可能にする readPixels について解説しました。
このメソッドは GPU と CPU 間での情報のやり取りを行うために GPU の動作をブロックするため、使い方を間違うと一気に描画が重くなります。使いどころはちょっと難しいですが、レンダリング結果から色情報を取得できるというのは非常に大きな意味があるので、ポイントを絞って活用してみてください。
さて今回は、今までありそうで意外なことにやっていなかったフラットシェーディングをやってみようと思います。
WebGL 用のラッパーライブラリとして非常に著名な three.js でも、フラットシェーディング風のレンダリングを行うことができますね。今回は WebGL のスクラッチ実装でフラットシェーディングを実現してみましょう。
フラットシェーディングがどんなものかわからない、という人はあまりいないかもしれませんが、もしそれがどんなものだかわからないようでしたら冒頭の画像をご覧になってみてください。従来のライティングの処理ではスムーズに陰影の濃淡がレンダリングされていたのに対し、フラットシェーディングではその名が示すとおりライトによる陰影付けがフラット(一様)になっています。要は、頂点単位ではなく、面を単位に陰影付けが行われたかのようになるのですね。
フラットシェーディングは、グラフィック表現におけるドット絵のように、ちょっとだけ古めかしいような、あるいは抽象的な、独特な雰囲気を演出する際に非常に有用な表現方法のひとつだと思います。表現力アップのためにも、ぜひチャレンジしてみてください。
面法線を使ったライティング
フラットシェーディングのレンダリング結果をよく観察してみると、これまでに当サイトで扱ってきたどんなライティングの結果とも異なる特徴があることがわかります。
当サイトのサンプルの多くは、グーローシェーディングやフォンシェーディングを使ってライティングの表現を行っていました。たとえば、頂点シェーダでライトによる陰影を計算してそのままフラグメントシェーダにこれを渡してやると、いい具合に自動的に線形で補間処理が行われるため、滑らかなグラデーションが効いた陰影が付きます。
グーローシェーディング
上記のようなシェーディング技法の場合、ライトの影響を計算する際に[ 頂点の持つ法線 ]の情報を利用します。頂点ごとに計算を行うわけですから、たとえば三角形であればそのプリミティブをレンダリングする際に3つの頂点から影響を受けて色が決まるわけですね。当然、グーローシェーディングなどの場合はこの3つの頂点の色が線形補間されるので、色が混ざったような風合いになります。これが従来のライティングの方法でした。
フラットシェーディングはよりはっきりとエッジが際立ったような見た目になりますが、これは法線とライトベクトルとの計算を頂点単位ではなく面単位で行うことで実現できます。三角形を構成するすべての頂点の法線が同じ方向を向いていれば、当然法線による計算結果も同じになります。それと同じ状況を作ってやればフラットシェーディングが行えるわけです。
面を構成する全ての頂点が同じ法線を持つようにモデルデータや頂点データを用意してやれば、当然普通にライティングの計算を従来通り行っても、結果はフラットシェーディングのような感じになります。ただ、そうなると既に持っている資産(モデルデータなど)を使い回すことができませんし、なんとかアプリケーション側でどうにかしたいところです。それに、正立方体のような単純な形状であっても、立方体の角にあたる座標位置では頂点定義が重複することになります。法線の情報を切り分けたいがために、全く同じ座標に何個も頂点を定義するというのはとても無駄です。複雑なモデルであれば、当然重複する頂点がより多くなるでしょうし、ストレージの意味でも難しい場合が出てくるかもしれません。
今回はこれらの問題に対応するために、WebGL の拡張機能を使います。一般にデリバティブ関数(derivative functions)と呼ばれる GLSL の機能を利用して、シェーダ側で動的に法線を求めます。
シェーダ内で動的に法線を求めるなんて、もしかしてすごく大変な計算が必要なのでは? と思ってしまう方もいるかもしれません。しかし、拡張機能を利用することで簡単に法線自体は求められます。いくつか注意すべきポイントなども踏まえつつ、次項からより詳細に見ていきましょう。
拡張機能を有効化するための手順
今回は拡張機能を使うことになるので、拡張機能に対応していないブラウザではうまく動かない可能性があります。ただ、今回利用する拡張機能に関しては、ほとんどのケースで問題なく使えると思います。
その拡張機能とは OES_standard_derivatives です。
この拡張機能を有効化できると、GLSL 内で、通常は利用できない特殊な関数が利用できるようになります。
// 拡張機能を有効化する
if(!gl.getExtension('OES_standard_derivatives')){
console.log('OES_standard_derivatives is not supported');
return;
}拡張機能の有効化はこれまでにも何度か登場しているので詳細については省きますが、今回の拡張機能の場合は gl.getExtension から戻り値を変数に取る必要はありません。有効化できたかどうかさえわかればいいので、上記のように記述すればいいでしょう。
また、MRT(Multiple Render Targets)のときに行ったのと同じように、GLSL 側にも拡張機能を利用するためのステートメントを追加します。
WebGL の拡張機能には WebGL だけで利用するものと、GLSL 側で利用するものがあります。GLSL 側で使うことになる拡張機能は当然ながら GLSL のコードの中にもそのことを明示する必要があるのですね。※一部、記載しないでも動く場合があるみたいですが、念の為に記載するようにしたほうがいいでしょう。
GLSL 側に追加するステートメント
#extension GL_OES_standard_derivatives : enableこのように #extension ディレクティブを使って、今回の拡張機能を確実に有効化させれば OK です。
拡張機能を有効化できると、GLSL の記述に dFdx と dFdy のふたつの関数が利用できるようになります。一見すると場当たり的に付けたいいかげんな変数みたいな名前ですがれっきとした GLSL の関数です。X 方向と Y 方向それぞれに関数が用意されていることがポイントになるでしょうか。
この dFdx や dFdy は、スクリーン空間上での偏微分を計算することができる関数です。
「へっ……へんびぶんッ!?」
となった方、安心してください。私もなりました(笑)
偏微分なんて難しそうな数学出てきたらお手上げだぜ! と匙を投げるのは簡単ですが、焦る必要はありません。もちろん、数学の知識がきちんとあって、偏微分の意味がわかる方はこの関数を用いることで様々なことが実現可能になることがわかると思います。そうでない場合は、ここでは数学のことはいったん忘れて、次のように覚えてしまいましょう。
dFdx や dFdy を用いることで勾配(傾き)が計算できる
これです。
これらの関数は、先程も書いたとおり[ スクリーン空間 ]でのみ利用できます。つまりフラグメントシェーダでのみ使えるというわけです。フラットシェーディングでは、頂点の座標情報をフラグメントシェーダ側で頂点シェーダから受け取り、それを元に頂点の勾配を計算します。勾配の計算は X 方向と Y 方向それぞれについて行いますので、そのために dFdx と dFdy というように、それぞれの方向用の関数が用意されているわけですね。
シェーダの記述
さて、それでは具体的にどのようにシェーダを記述すればいいのか見ていきます。
まず大事なポイントとして、今回のシェーダでは頂点属性としての法線はシェーダで受け取らないようにします。もちろん受け取ったらダメということではないのですが、フラットシェーディングを行うためにデリバティブ関数を使うことになるので、法線については attribute 変数として取得しなくても、動的にシェーダ内で計算してやることでライティングを行うことができるのですね。
そのことを踏まえて、頂点シェーダのコードから見てみます。
頂点シェーダ
attribute vec3 position;
attribute vec4 color;
uniform mat4 mMatrix;
uniform mat4 mvpMatrix;
varying vec4 vPosition;
varying vec4 vColor;
void main(void){
vColor = color;
vPosition = mMatrix * vec4(position, 1.0);
gl_Position = mvpMatrix * vec4(position, 1.0);
}先述のとおり、attribute 変数としては座標と、色、だけが javascript から送られてくるようになっています。
そして、uniform 変数としては行列をふたつ、受け取るようにしています。ここで登場する行列のうち mMatrix のほうはモデル座標変換行列ですので注意してください。どうしてモデル座標変換行列が必要になるのかは、今回実現しようとしている処理の内容をよく考えてみれば自ずとわかると思います。フラットシェーディングを行うために、頂点の座標情報から勾配を計算することが今回の目的です。となると、フラグメントシェーダ側でモデル座標変換後の頂点がどんな座標にいるのか、その情報が必要になるわけです。上記の例では、varying 変数 vPosition にモデル座標変換後の頂点座標の位置を代入し、フラグメントシェーダへと渡しています。
さて、続いてはフラグメントシェーダです。
フラグメントシェーダでは実際に勾配を計算するコードを記述していきます。しかし、ここはそれほど難しくはありませんので、落ち着いて見ていきましょう。
フラグメントシェーダ
#extension GL_OES_standard_derivatives : enable
precision mediump float;
uniform vec3 lightDirection;
varying vec4 vPosition;
varying vec4 vColor;
void main(void){
vec3 dx = dFdx(vPosition.xyz);
vec3 dy = dFdy(vPosition.xyz);
vec3 n = normalize(cross(normalize(dx), normalize(dy)));
vec3 light = normalize(lightDirection);
float diff = clamp(dot(n, light), 0.1, 1.0);
gl_FragColor = vec4(vColor.rgb * diff, 1.0);
}フラグメントシェーダ側では、先程から何度か話題に上がっている dFdx などを使った処理を記述します。これらの関数は与えられたベクトルから勾配を計算して返します。
上記のコードの main 関数冒頭を見てみましょう。頂点シェーダから送られてきた、モデル座標変換後の頂点の座標を元にして勾配の計算が行われているのがわかると思います。このような処理を経たあと、スクリーン空間上の X 軸方向に対して得られた勾配が変数 dx に、同様に Y 方向の勾配が変数 dy に取得できます。
ここで得られたふたつの勾配から、法線に相当する情報を得るために外積を使っている箇所があります。以下、抜粋したコードです。
該当箇所を抜粋
vec3 n = normalize(cross(normalize(dx), normalize(dy)));ここで登場している cross というのが外積を行うためのビルトイン関数ですね。三次元ベクトルの外積では、ふたつのベクトルに対して直交するベクトルが得られます。その性質を利用して、面法線に相当するベクトルを算出しています。上記のコードでいちいち正規化を行っているのは、今回のケースの場合はあくまでも方向に注目しているので、ベクトルの大きさが邪魔だからですね。正規化を正しく行っていないと、モデルデータが極端に大きい、または小さいなどの場合にうまくレンダリングできなくなる可能性が高いので気をつけましょう。
ちなみに、ここで計算された面法線に相当する情報(上記で言う変数 n の中身)をそのまま色として出力してみると、以下のような感じになります。
勾配計算した結果を色として出力

ここまでくれば、あとはこのフラットな法線を使ってライティングを行えばいいですね。
まとめ
さて、少々駆け足気味でしたが、フラットシェーディングの実装については理解できたでしょうか。途中、外積を使った面法線に相当するベクトルの算出など、ちょっと 3D 数学に不慣れだとわかりにくいような概念も出てきましたが、焦らずじっくり、必要に応じて調べたり振り返ったりしながら考えてみていただければと思います。
その昔、まだまだ 3DCG 自体が誕生したばかりのころは、計算負荷の観点から、当時の手法としては負荷の少ない実装であるフラットシェーディングが使われていました。それが現代では、フラットシェーディングを実現するには逆に計算の負荷という代償を払わなければならないというのが、なんとも因果ですね。
今回利用したデリバティブ関数は、フラットシェーディングの実現の他にも、たとえばアンチエイリアシングなどを行うためによく利用されています。勾配の計算、と言われてもいまひとつピンとこないかもしれませんが、高速なシェーダ内でこういった計算が行えるというのは、いろんな処理の幅を広げるという意味では面白いなあと思います。
あまり頻繁に使う技術ではないかもしれませんが、気になる方はぜひチャレンジしてみてください。
今回も、実際に動作するサンプルは以下のリンクから参照できます。
