マウス座標による回転

今回のサンプルの実行結果
クォータニオンを何に使うか
前回は、当サイトのオリジナルライブラリである minMatrixb.js を用いて、クォータニオンを扱う方法について解説しました。
カメラの座標とカメラの上方向という二つのベクトル要素をクォータニオンで回転させることによって、モデルを見つめたまま周囲を回るカメラの挙動を実現しましたね。今回はその延長線上の処理の一つとして、マウスの座標をリアルタイムに取得しながら、それに応じてモデルを回転させる処理を実装してみます。
今回のサンプルで最も大きなポイントとなるのは、前回のサンプルが、あくまでもベクトルにクォータニオンを適用する処理であったのに対し、今回のサンプルは行列にクォータニオンを適用する処理であるという点です。
今回も、前回同様 minMatrixb.js を使ってクォータニオンを操作します。ですから、数学的な知識がそこまで深くなくても、実装すること自体は比較的簡単です。焦らずじっくり考えてみてください。
マウス座標をもとにした回転
javascript には、ブラウザ上で起こるイベントをトリガーにして処理を行なう方法がいくつかあります。今回のサンプルでは addEventListener メソッドを使って、マウスイベントを捕捉しながらレンダリングを行ないます。
具体的には、canvas 上でマウスが動いたときに発生する onmousemove イベントに処理を登録し、リアルタイムにマウスの座標を取得するようにします。取得したマウス座標をもとに回転軸ベクトルと回転角を割り出し、そこからクォータニオンを生成します。
回転を与えられたクォータニオンが準備できたら、そのクォータニオンを座標変換行列に適用します。ここが、前回のサンプルと大きく違う部分です。前回はクォータニオンを適用する対象がベクトルでしたが、今回はモデルに回転を適用するため、モデル座標変換行列に直接クォータニオンを適用するわけです。
やるべきことのだいたいの流れは理解できたでしょうか。
ちょっと駆け足ですが、早速実際のコードを見ていきましょう。
まず、今回はマウスのイベントに関する処理を記述する都合上、今までとは違いグローバルな変数に canvas タグへの参照を得るようにします。
これは、マウスイベントの処理のなかで、canvas タグに関する情報を利用するからです。
さらに、マウスのイベントとして登録する処理のなかでは、マウスの座標を取得し、そこから回転軸ベクトルと回転角を算出するという作業を行ないます。ここまでを抜粋したのが以下のコード。
グローバル変数とマウスムーブイベントの定義
// canvas とクォータニオンをグローバルに扱う
var c;
var q = new qtnIV();
var qt = q.identity(q.create());
// マウスムーブイベントに登録する処理
function mouseMove(e){
var cw = c.width;
var ch = c.height;
var wh = 1 / Math.sqrt(cw * cw + ch * ch);
var x = e.clientX - c.offsetLeft - cw * 0.5;
var y = e.clientY - c.offsetTop - ch * 0.5;
var sq = Math.sqrt(x * x + y * y);
var r = sq * 2.0 * Math.PI * wh;
if(sq != 1){
sq = 1 / sq;
x *= sq;
y *= sq;
}
q.rotate(r, [y, x, 0.0], qt);
}後述しますが、今までのサンプルと同じように、WebGL 関連の多くの処理は window.onload の中に記述します。上記のコードでは、canvas タグへの参照を取得する変数 c と、回転を与えたクォータニオンを格納する変数 qt がグローバルな変数として宣言されていますね。ここでグローバルな変数として宣言している理由は、 window.onload に記述した処理とマウスムーブイベントの双方とで、同じ変数を参照できるようにするためです。
マウスムーブイベントに登録する処理の中でなにをやっているのかは、一見するとわかりにくいかと思います。要は canvas の中心点からマウスポインタまでの相対的な位置を調べて、そこから軸ベクトルと回転角を算出する処理を行なっています。
上記のコードで言えば、変数 r が回転角に相当する部分であり、変数 x と変数 y が、canvas の中心点から見たマウスポインタの相対位置です。
上記の mouseMove という関数の最後の行では、クォータニオンに回転を与える処理を実行していますね。ここでは rotate メソッドの第二引数に、X と Y の値を逆転させて指定していますが、こうすることで軸ベクトルを正しく渡すことができます。
ここまでの処理は、コードだけを見てもイマイチ意味がわからないと思います。非常に簡単にですが、ここでやっていることを図案化すると次のような感じです。
まず、マウスポインタの位置が、キャンバス上における以下の図の (a, b) の位置にあるとします。
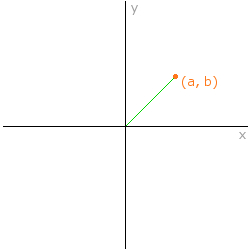
原点から、マウスポインタの座標位置に向かってまっすぐ伸ばした線が、緑色をした線分ですね。
このとき、この緑色の線分と垂直なもう一つの線分を考えます。
その垂直な線分が、以下の図で言うところのピンク色の線ですね。
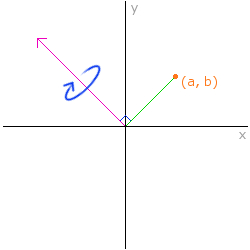
このピンク色の線分を軸として回転を行なえば、マウスポインタの位置に応じた任意の回転が得られるということはわかると思います。
つまり上記の図でピンク色で表されているものこそが、回転の軸ベクトルになるんですね。これを正規化してから、クォータニオンに回転を与える rotate メソッドに渡してやればいいことはなんとなくわかっていただけたでしょうか。
回転角は、純粋にベクトルのノルム、つまり大きさから判断すれば算出できます。先ほどのコードの中で言うと、変数 sq 周辺の処理が、この回転角を算出するための処理になります。
どうしても数学的な話になるので理解しにくいかもしれませんが、じっくりと考えてみてください。
マウスイベントの登録など
先述の、マウスポインタから得た座標を使って回転軸ベクトルと回転角を算出する処理を、マウスイベントとして登録します。
イベントを登録する際には、先ほども書いたとおり javascript の addEventListener を使います。
イベントを登録する
// canvasエレメントを取得
c = document.getElementById('canvas');
c.width = 300;
c.height = 300;
// canvas のマウスムーブイベントに処理を登録
c.addEventListener('mousemove', mouseMove, true);canvas への参照を取得した後、 addEventListener メソッドを使って先ほど記述した mouseMove という関数を onmousemove イベントに登録します。
canvas 上でマウスポインタを動かすとマウスムーブイベントが発生するので、そのたびに mouseMove 関数が走るようになるわけです。これで、リアルタイムにマウスポインタの座標からクォータニオンを生成することができるようになりましたね。
あとは、ここで生成したクォータニオンを使って、恒常ループのなかでモデルを回転させてやる処理を行なえばいいわけです。何度も書いているように、今回はクォータニオンを行列に適用することによって、座標変換行列そのものをクォータニオンによって変換します。
クォータニオンを行列に適用する処理も、当サイトのオリジナルライブラリ minMatrixb.js を使えば簡単に実装できます。そのためのヘルパーメソッドが qtnIV.toMatIV メソッドになります。
このメソッドは、4 x 4 の正方行列に対してクォータニオンを適用します。
qtnIV.toMatIV メソッドの記述
// クォータニオンを行列に適用
var qMatrix = m.identity(m.create());
q.toMatIV(qt, qMatrix);このようにすると、変数 qMatrix はクォータニオンによる回転が適用された状態の座標変換行列になります。あとは、ここで生成した行列を使ってモデルを座標変換すればいいですね。
以下、恒常ループ内の一部を抜粋します。
恒常ループ内処理の一部を抜粋
// カウンタをインクリメントする
count++;
// カウンタを元にラジアンを算出
var rad = (count % 180) * Math.PI / 90;
// クォータニオンを行列に適用
var qMatrix = m.identity(m.create());
q.toMatIV(qt, qMatrix);
// モデル座標変換行列の生成
m.identity(mMatrix);
m.multiply(mMatrix, qMatrix, mMatrix);
m.rotate(mMatrix, rad, [0, 1, 0], mMatrix);
m.multiply(tmpMatrix, mMatrix, mvpMatrix);
m.inverse(mMatrix, invMatrix);
// uniform変数の登録と描画
gl.uniformMatrix4fv(uniLocation[0], false, mvpMatrix);
gl.uniformMatrix4fv(uniLocation[1], false, mMatrix);
gl.uniformMatrix4fv(uniLocation[2], false, invMatrix);
gl.uniform3fv(uniLocation[3], lightPosition);
gl.uniform3fv(uniLocation[4], camPosition);
gl.uniform4fv(uniLocation[5], ambientColor);
gl.drawElements(gl.TRIANGLES, torusData.i.length, gl.UNSIGNED_SHORT, 0);
// コンテキストの再描画
gl.flush();今回のサンプルは、以前やった点光源によるフォンシェーディングを使いますので、HTML やシェーダに関しては、そのときのものをそのまま使いまわしています。
ここでのポイントは、マウス関連の処理によってリアルタイムに更新されるクォータニオンを使って、モデル座標変換行列に回転を与えているということですね。モデル座標変換ではその掛け合わせる順序に気をつけましょう。今回の場合、まず最初にループごとにインクリメントされるカウンタを使ってラジアンを算出し、このラジアンを使って Y 軸を中心にモデルを回しています。
その後、クォータニオンを適用した行列をさらに掛け合わせることによって、マウスポインタの位置に応じた回転を適用しています。
まとめ
恐らく、今回のサンプルで一番難しいのは、マウスポインタの座標からクォータニオンを生成する部分ではないかと思います。ここはどうしても数学的な知識が若干必要になります。
あえて難しいことは考えず、コードをそのままコピーしても構いません。ただ、どうしてこのような処理で回転軸ベクトルと回転角が算出できるのか、それを深く考えてみることも無駄にはならないでしょう。
回転を適用したクォータニオンを作ることに慣れておくと、あとあと必ず役に立つはずです。ちょっと難しいかもしれませんが、是非コードを読み解いてみてほしいと思います。
サンプルへのリンクはいつものように下のほうにあります。
実際にサンプルを動作させ、マウスポインタの位置に応じて自由自在に回転するモデルを確認してみてください。
次回は、クォータニオンの便利な使い方の一つ、球面線形補間について解説します。
