箱型のボックスモデルを描く

今回のサンプルの実行結果
球体以外のモデルを描く
前回は同じ形状のオブジェクトを複製することで、スクリーン内にたくさんのオブジェクトをレンダリングする方法を解説しました。
等間隔に複数の同一形状オブジェクトをレンダリングできる repetition ですが、使いどころはなかなか難しいかもしれません。とはいえ、割と簡単なコードの追加だけで実装できるので、ぜひ挑戦してみてください。
さて、今回は今までずっと球体のみで話を進めてきましたので、ちょっと違う形状のレンダリングにチャレンジしてみましょう。今回は箱型のボックスモデル(立方体)をレンダリングしてみたいと思います。
レイマーチングでは、どのような形状をレンダリングするのかは distance function の実装次第です。今回もそれほど複雑なコードにはなりませんので、じっくりと取り組んでみましょう。
まずはコードを見てみる
さて、それでは少々駆け足ですが、まずは問題の distance function のコードだけを抜粋して見てみます。
ボックスモデルの distance function
float distanceFunc(vec3 p){
vec3 q = abs(trans(p));
return length(max(q - vec3(0.5, 0.5, 0.5), 0.0));
}はい、このように実にシンプルでコードの量はそれほど多くありません。その気になれば一行でも書ききれてしまう程度の量ですね。
今回のサンプルも、前回と同様に repetition を行う trans が登場していますが、もちろんこれを噛ませなくてもちゃんと動きます。
ボックスモデルの distance function でポイントとなるのは length の中で処理されている vec3 のパラメータでしょうか。今回は X Y Z のいずれも 0.5 を指定していますが、この部分がレンダリングされる立方体の形状を決めています。
たとえば、X を大きな値にすれば横に幅広い立方体になりますし、同様に Y を大きな値にすれば縦に長い立方体になります。上記のサンプルコードのようにすると、形状としては各辺の長さが 1.0 の正立方体になりますね。球体の場合と違う点に着目して考えると、ビルトイン関数の max を使っているということが最大の違いだと思います。
コードをよく見て考えるとわかると思いますが、distance function のなかでは、まず最初に abs を使って絶対値を取ってから、先述の vec3 で定義した立方体のデータを減算しています。引数として受け取った座標次第では、この減算処理によって負の数値になってしまう場合も考えられますが、 max を通すことで 0.0 より小さな値になってしまうことはありません。
しかし、このようなコードでどうしてボックスモデルがレンダリングされるのでしょうか。
なるべく単純化してロジックを読み解く
今回も、例によってすごく単純化して考えてみることが理解への近道です。
たとえば、X だけに要素を絞って考えてみましょう。もし、distance function に渡されたレイの先端座標が -1.0 ~ 1.0 の範囲だったと仮定しましょう。この場合、最初の abs によって、負の数値は強制的に正の値に変換されますので、変数 q の中に入る値の範囲は 0.0 ~ 1.0 の範囲に収まるはずです。ここまでは簡単ですね。
続いて、その変数 q に対して減算する処理が発生しますが、今回のサンプルの場合はここで 0.5 を引いています。ということは、その結果は -0.5 ~ 0.5 の範囲になるはずですが max によって値が変換されるので、得られる答えは 0.0 ~ 0.5 の範囲になるということがわかるでしょう。
実際には、このような計算が X Y Z の各軸に対して行われたあと、その結果得られたベクトルが length によって処理されます。
ベクトルの大きさの計算方法は例によって割愛しますが、ここまでわかればどうしてこのような計算によって箱型のモデルがレンダリングされるのかは理解できるのではないでしょうか。
もし、ここまで読んでみてもいまいち理解できないようでしたら、紙に X と Y の二つの軸だけでいろいろと図解して計算してみると、わかりやすいと思います。要するに、ざっくりとした考え方としてはレイの座標が一定以下の数値になるとき、max 関数の効果で負の数値が 0.0 に丸められるため、distance function から返される値が 0.0 かそれに非常に近い数値になるということです。
できるだけ、単純化して考えてみてください。
今回はちょっと図解するのが難しかったので文章だけでの解説になってしまいましたが、自分で紙などに図解して、順を追って処理内容を考えていけばきっと理解できると思います。
ボックスモデルを応用した角丸ボックス
さて、今回はもうひとつ、角の丸いボックスモデルについても見てみましょう。
今回のテキストの冒頭のキャプチャ画像は、今から説明する角丸のボックスモデルを用いたレンダリング結果です。
まず、前項の角を取っていない普通のボックスモデルをレンダリングした結果を見てみます。
角丸ではない普通のボックスモデル

このように、しっかりと角の立った立方体が描かれています。
ライトベクトルの向きが前回とはちょっと違っていますが、ちゃんと面法線によって正しく陰影も付いているのがよく見るとわかりますね。
さて、このようなボックスモデルのレンダリング結果が、先ほどの distance function にほんの少しのコードを書き足して修正するだけで、以下のような角丸のボックスモデルに変わります。
角丸のボックスモデル

キレイに角が丸まっているのがわかりますね。
先ほども書いたように、distance function に対して行う修正は本当にわずかです。
これは、実際にコードを見てもらえればわかるでしょう。
角丸ボックスの distance function
float distanceFunc(vec3 p){
vec3 q = abs(trans(p));
return length(max(q - vec3(0.5, 0.5, 0.5), 0.0)) - 0.1;
}さて、どうでしょう。
修正されている場所がわかりましたか?
正解は戻り値から 0.1 を引くだけです。恐ろしく簡単ですね。
たったこれだけで、どうして角が取れて丸くなるのか……不思議ですよね。
最終的な戻り値(length の計算結果)からさらに減算処理するということは、球体のときの distance function でやったのと同じようなことが起こっていると考えることができます。
distance function に渡された座標が、オブジェクトより少しだけ外側にあってそのままでは実際には衝突しないというケースであっても、最終的に減算処理を行っていることによってあたかも衝突しているのと同じような計算結果になってしまうわけです。
減算によって角が丸くなる概念図
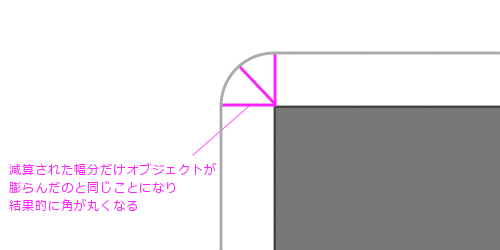
この考え方に則ってみれば、減算する値を大きくすればするほど、ボックスモデルが膨らんでいくということがわかりますね。
ためしに、減算する値を 0.1 から 0.5 に変更してみると、以下のように太ましい感じのボックスモデルが生成されます。
さらに減算したボックスモデル

まとめ
さて、今回は最も基本的な球体という図形の次の一歩ということで、箱型のボックスモデルについて解説しました。
幾何学的な図形の代表格と言ってもいいボックスモデル。ほんの少しのコードの追加で、角を取ったような形状になったりして非常に面白いですよね。
レイマーチングにおける distance function は、基本的な図形は本当にシンプルかつ極めて少ないコードだけで表現できます。こういった基本的な図形の概念にたくさん触れて慣れておくことで、さらに応用を利かせた複雑な図形へチャレンジするための基礎が磨かれていくのだと思います。
少々難しい部分もあるかもしれませんが、それでも放り投げたくなるほど難しいものではなかったと思います。諦めずに、じっくりと取り組んでみてください。
実際に動作するサンプルはいつものように以下のリンクから。
