スフィア環境マッピング(Matcap Shader)

今回のサンプルの実行結果
手軽な環境マッピング
前回は、インターリーブ配列を用いて VBO を生成することで、効率よくレンダリングを行う方法について解説しました。
WebGL ではものすごくシビアな調整が求められるシーンはまだそれほど多くないのかもしれません。というより、その次元まで到達している利用者が少ないのだと思いますが、それでもこういった低レイヤな部分の処理についても少しずつ勉強しておくと、いつか役に立つ日がくるかなと思います。無理なく、少しずつでも挑戦してみてください。
さて、今回は前回とは少し趣向を変えて、スフィア環境マッピング(Matcap Shader)にチャレンジしてみましょう。
WebGL には、キューブ環境マッピングと呼ばれる環境マッピングの仕組みがあらかじめ備わっています。こちらはその名のとおりキューブ状にテクスチャが配置されていると仮定しテクセルを参照することで、周囲の風景が映り込んだかのような外見を得ることができる手法です。既に当サイトでも何度か登場していますね。
それに対してスフィア環境マッピングとはいかなる技術なのでしょう。
スフィア環境マッピングは、こちらも名前からどのような技術なのか想像ができますね。キューブ環境マッピングとは違い、球を模したテクスチャから色を読み出し、これを利用して環境マッピングを実現するのがスフィア環境マッピングです。こちらは WebGL の基本機能としてサポートされているわけではありませんが、実装自体はそれほど難しくありません。少しだけ 3D 数学の話が出てきますが、どちらかというとキューブ環境マッピングよりも単純な実装だと言えると思います。
今回はそんなスフィア環境マッピングの実現について見ていきたいと思います。
Matcap テクスチャ
さて、スフィア環境マッピングの実現に欠かせない要素のひとつである、テクスチャ素材についてまずは考えてみましょう。
スフィア環境マッピングでは球体のような特殊なテクスチャを参照します。これは一般に Matcap などと呼ばれることが多いですが、実はこの Matcap という言葉は略称です。正確には「Material Capture」ですね。
マテリアルを、キャプチャしたもの、つまり、Matcap とは「オブジェクトの質感が焼き込まれたテクスチャ」だと考えるといいと思います。このような質感を事前に焼き込んだテクスチャを利用することによって、比較的簡単に風景の映り込みやオブジェクトの表面の質感表現を行ってしまうというのがスフィア環境マッピングの考え方です。
Matcap 素材は様々なところで配布されていたり、モデリングソフトのリソースとしてあらかじめ組み込まれていたりしますが、がんばって自分で撮影したものを利用したり、画像処理を駆使して用意したりすることができます。
Matcap 素材の一例
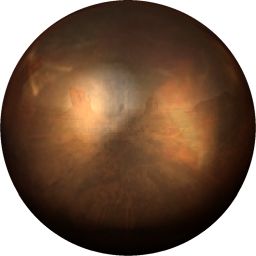
これを見るとわかるとおり、Matcap は球体を描画したような見た目をしています。
風景の映り込みや特殊な質感をシェーダだけで実現するのはそこそこ大変ですし、なにより演算の負荷が高くなってしまうケースも多いわけです。その点、Matcap を参照して質感を近時できるスフィア環境マッピングは、比較的計算の負荷が低いこともあって、かなり昔から存在するテクニックです。
スフィア環境マッピングの理屈
さて、スフィア環境マッピングが特殊なテクスチャを参照して、質感を近似して表現する方法であることはわかりました。
しかし実際に、どうやってテクスチャを参照してやればいいのでしょうか。
スフィア環境マッピングを理解するということは、スフィア環境マッピングを用いる際に「どのようにテクスチャ座標を決定するか」を理解するのと同じです。球のような模様をしているテクスチャから、いったいどのようにテクスチャ座標を決定して色を読み出せばいいのでしょう。
実は、スフィア環境マッピングのキモとなるテクスチャ座標の算出は、考え方自体はとても単純です。たとえば、シーンのなかに球体のモデルがひとつ置かれている状態をイメージしてみましょう。この球体を撮影するカメラが Z 軸上にあり、原点に置かれている球体に向かって向けられているとします。
球体を見つめるカメラ

この球体に、仮にスフィア環境マッピングを正しく適用することができた場合、最終的にスクリーンに描き出されるレンダリング結果はどのようなものになるでしょうか。
頭を柔らかくして、考えてみましょう。
正しくスフィア環境マッピングが成功した場合は、まるで、球体の表面にそのままテクスチャを投影したような見た目になるはずです。
正しく投影できた場合のイメージ

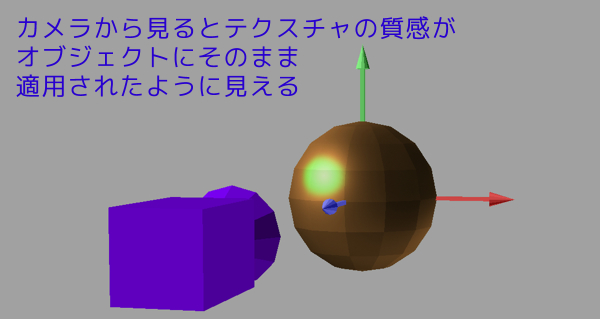
さて、どうでしょうか。ここまで読んで、テクスチャ座標の算出方法に察しがつくでしょうか。
上の図を見てよくよく考えてみると、頂点属性として非常になじみ深い、あの属性値がそのままテクスチャ座標として使えそうな気がしてきませんか?
その属性値とは、頂点法線です。
球体にスフィア環境マッピングを適用した場合、ちょうど法線が、原点を中心に持っていった状態のテクスチャ座標のような値になっているんですね。もちろん法線は XYZ の値を持つ三次元ベクトルですが、今回の場合は Z 値については無視することができます。XY をそのままテクスチャ座標 ST として使えばいいわけです。
また、本来法線は負の数値を含む可能性のある属性値ですが、テクスチャ座標は 0.0 から 1.0 で表しますよね。このことから、法線の XY 要素をテクスチャ座標用に変換して利用すれば良さそう、ということが想像できます。この変換は非常に簡単で、単に法線に 1.0 を足して 2 で割るだけですね。
おお、やったぞこんなに簡単にスフィア環境マッピングは実現できるのか! と思わず歓喜の声を上げたくなってしまいますが、そうは問屋がおろさないのが 3D の世界。
単純に法線に 1.0 足して 2.0 で割って、それをテクスチャ座標として使っただけでは実際にはうまくいきません。
世界は回る、モデルも回る
さて、法線からテクスチャ座標に変換するだけでうまくいかないとは言われても、どううまくいかないのかは、頭の中だけではイメージしにくいですね。
仮に、シェーダで法線からテクスチャ座標を算出してそのまま使うと、以下のようなことが起こります。
モデルを回転させた場合の図

当たり前ですが、モデルは回転や拡大縮小、平行移動などのモデル座標変換が適用される場合があります。というか、普通しますよね。
そうすると当然ながら必ずしもカメラから見た法線の状態が、スフィア環境マッピングに適した状態ばかりとは限らないわけです。
さらに言えば、モデルだけでなく、カメラが動く場合も考えられます。カメラが動いたりすれば、当然世界がどう見えるかも変わりますし、法線とカメラの関係も変わってきます。そのあたりを諸々考慮すると、法線をそのままテクスチャ座標に単純に変換しただけでは、うまくいかない場合のほうが多いということがわかりますね。
なかなか難しいですね。
ここでもし「全然難しくないだろ」と思った方は、恐らく自分でスフィア環境マッピングを軽く実装できる方なのだと思います。少なくとも私は最初「どうしたらええねん! 数学わからんわ!」と思いました。
すごく物事を単純化して考えてみると、今回の場合、要は「カメラから見た法線」の状態が、常に「Z 軸上のカメラから見たのと同じ状態」になっていればいいわけです。最初に出てきた「球体を Z 軸上のカメラから見つめている状態」とまったく同じ条件になるように法線を変換することができれば、スフィア環境マッピングが実現できるはずですね。
どこから見ても Z 軸上カメラから見たのと同じにする

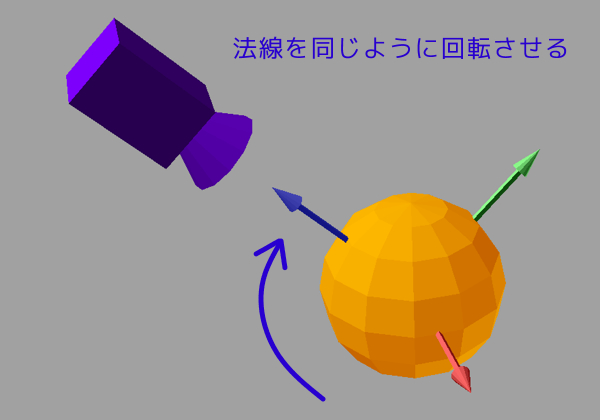
言い換えると、こういうふうにも表現できます。
要は何かしらの方法で法線を変換して、常に「スクリーン空間の XY 方向と法線の XY 方向が完全に重なっている状態」を作ればいいのです。
これを実現するためには、行列を使って法線を変換してやります。通常、ライティングなどを実現する際に法線を変換する場合は、モデル座標変換行列の逆転置行列 を使いますね。今回の場合は、カメラの影響を考慮する必要がありますので、モデル座標変換行列ではなく、モデル x ビュー行列の逆転置行列 を使います。
このような行列を利用して法線を変換すると、まるでビルボードのように、常にカメラの方向に対して固定される法線の状態を再現できます。
カメラの方向にも、モデルの回転などにも影響を受けない、スクリーンの XY と法線の XY の方向が完全に一緒になる状態さえ作り出せれば、あとは法線の XY に 1.0 を足して 2 で割るという最初のロジックを適用し、スフィア環境マッピングが実現できます。
これらのことを踏まえつつ、シェーダのコードを見てみましょう。
スフィア環境マッピングシェーダ
// 頂点シェーダ
attribute vec3 position;
attribute vec3 normal;
uniform mat4 mvpMatrix;
uniform mat4 normalMatrix; // モデルビュー逆転置行列
varying vec3 vNormal;
void main(void){
vNormal = normalize((normalMatrix * vec4(normal, 0.0)).xyz);
gl_Position = mvpMatrix * vec4(position, 1.0);
}
// フラグメントシェーダ
precision mediump float;
uniform sampler2D texture;
varying vec3 vNormal;
void main(void){
vec2 texCoord = (vNormal.xy + 1.0) / 2.0;
vec4 smpColor = texture2D(texture, vec2(texCoord.s, 1.0 - texCoord.t));
gl_FragColor = smpColor;
}頂点シェーダで normalMatrix という名前になっているのが、モデルビューの逆転置行列です。これで法線を変換して、フラグメントシェーダへと渡します。
フラグメントシェーダのほうでは、法線の値に 1.0 を足してから 2 で割ります。こうすることで、負の値だった法線も、正しくテクスチャ座標として使える状態になります。その上で、テクスチャを参照して色を取り出します。
シェーダは頂点シェーダ・フラグメントシェーダのいずれもとても簡単ですね。こんな簡単なシェーダで実現できるスフィア環境マッピングは、非常にシェーダの負荷が低いタイプの処理と言っていいのではないでしょうか。
まとめ
一見万能に見えるスフィア環境マッピングですが、実際に動作するサンプルなどを見てみるとわかると思いますが、常にカメラに対して映り込む風景が固定されます。これはカメラに対して法線が固定されるような変換をしているわけですから、当たり前です。
常にマッピングは固定される

たとえば、部屋の内装を撮影したようなスフィア環境マッピング用のテクスチャを使った場合、カメラを動かしてしまうと、本来なら映り込まないはずの位置に、風景が映ってしまう場合が考えられます。例えるなら、現実なら天井が映り込むような角度からカメラを向けても、映り込んで見える風景は Z 軸上の正面から眺めた場合とまったく同じなのですね。
つまりスフィア環境マッピングでは、カメラを動かしてしまった場合にはいろいろよろしくない状態が起こります。一方、キューブ環境マッピングではこのような問題は起こりません。WebGL は既定でキューブ環境マッピングをサポートしていますので、厳密な映り込みを環境マッピングで再現したい場合には、キューブ環境マッピングを使うべきでしょう。
とは言え、非常に簡単な実装で実現できるスフィアマッピングは、気軽に質感を変えることができる技術としてはとても有用だと言えますね。計算の負荷もそれほど高くないので、使いこなせれば真面目にライティングの計算をするよりもかなり軽量なシーンを実現できるはずです。なにより、なんとなく見た目がカッコいいですよね。映り込みは。
サンプルは以下のリンクから参照できます。今回は効果をわかりやすくするための球体とトーラスで実行した場合、さらにスタンフォードバニーのモデルで実行した場合を用意しています。
