行列(マトリックス)の基礎知識
お店の前にできるあれではなくて
リアルタイム 3D レンダリングの世界では、行列が頻繁に登場します。
ここで言う行列とは、数学的な意味での行列です。英語で言うと Matrix (マトリックス)ですね。
一口に行列と言ってしまえば簡単そうに聞こえますが、行列にも様々な種類がありますし、その計算方法はそれなりに難解というか面倒です。簡単に言葉として説明してしまうと、行列とは数字を並べた箱のようなイメージのもので、文字通り数字が縦横に行列を形成しています。行列は普段の生活のなかではまずお目にかかることがないものだと言えますが、3D レンダリングの世界においては欠かせない存在のひとつです。
なぜ行列が必要なのか
行列が 3D レンダリングの世界に欠かせない存在だと言われても、いまいちピンとこない人もいるでしょう。そもそも、どうして行列がそこまで取り沙汰されるのでしょうか。
三次元空間をシミュレートすることには、非常に多くの計算が必要になります。どんなモノが、どこに、どんな角度で、どんな大きさで存在するのか、それを描画したいモデルの数だけ計算しなければならないわけですから、非常に複雑で尚且つ大量の演算を行なわなければなりません。
行列は、先ほども書いたように数字が行列を成すような形で並べられた、数字の詰め合わせのようなイメージです。実はこの行列を使うことによって、一つの行列のなかにたくさんの情報を詰め込むことができます。
たとえば、描画したいモデルが、世界のどこに置かれているか、置かれているとしてそれが回転したり、あるいは拡大縮小したりしているのか、それを撮影するカメラはどこにあって、どこを向いていて、最終的に撮影されたものが映し出される面の縦横の比率はどうなっているのか……とか、いまざっと並べたような情報を、行列を使うことによってギュッとひとつにまとめることができてしまいます。
そして、以前のテキスト(3D 描画の基礎知識)を読んだ方で、勘のいい人なら気がついたはずです。
モデルを世界のどこに置くかとか、カメラの向きがどうこうとか、そういう話は以前にも出てきましたよね。
そう、つまりは、モデル座標変換・ビュー座標変換・プロジェクション座標変換の、一連の座標変換を行列を使って処理することによって、最終的にはたった一つの行列で全ての座標変換の結果をまとめて処理することができるようになります。なんとなくですが、行列がどうして必要なのか、イメージできたでしょうか。要は、行列は非常に計算効率が良く、ものすごく便利ってことです。
3D レンダリングと行列
さて、行列は数字の詰め合わせであるなどと安易に書きましたが、実際に行列とはどのようなものなのでしょうか。
行列には様々な種類がありますが、その一つに正方行列があります。これは、行列の行と列が同じ要素数になっている行列のことです。
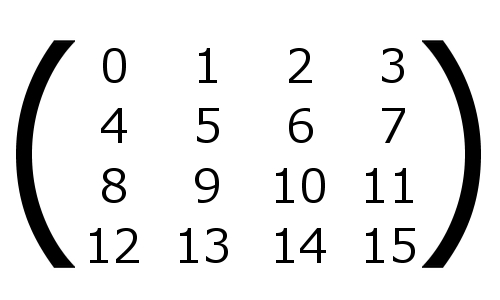
上記のような行列を、正方行列と呼ぶわけですね。※中身の数字は適当ですのであしからず
さて、この正方行列ですが、一般的な 3D レンダリングの世界では 4 x 4 の行列を用いるのが一般的です。先ほどの行列の図は、行と列がそれぞれ四つずつの要素で成り立っていたので、まさにこの形が 3D レンダリングの世界で使われる行列の形ですね。
3 x 3 の正方行列や、あるいはその他の行列ではなく、どうして 4 x 4 の正方行列を使うのかについてはきちんと理由があります。ですが現時点では気にする必要はないと言っていいでしょう。行列は 3D レンダリングの計算に使うことができる便利な仕組み、とでも覚えておけば、まずは問題ありません。
というのも、行列は完全に数学の世界の話なので本当にしっかりと理解しようと思うと非常に大変です。ちゃんと学んだほうがいいのは間違いありませんが、今の段階ではざっくりと、なんとなく行列というものがどんなものなのかわかっていれば十分です。※実際問題、私自身も数学を専攻したわけではありませんし、行列の隅々までを完全に理解しているわけではないですしね
実際の 3D レンダリングに際しては、先述のとおり、モデル座標変換・ビュー座標変換・プロジェクション座標変換のそれぞれに行列を用います。具体的には、それぞれの座標変換を表す行列を個別に用意し掛け合わせます。そうして最終的に出来上がった変換行列を WebGL の頂点シェーダに渡します。
頂点シェーダは渡された座標変換行列を元に、描画するモデルの座標を変換して、画面に映し出せる状態に加工します。つまり、座標変換行列を操作することで、モデルをどのように描画させるのかを変化させることができるのですね。
行列によってできること
以前のテキストでも解説したように、座標変換にはいくつかの種類があります。モデル変換、ビュー変換、プロジェクション変換がそれに相当します。
行列は、上記のそれぞれの変換についての情報を保持することができ、たとえばモデル変換行列であれば、描画したい 3D モデルの位置や、拡大縮小の有無、そして回転しているかどうかなどを一つの行列で定義できます。
ビュー変換行列ではカメラの位置やカメラの向き、そしてカメラがどこを見ているのか(注視点)などを一つの行列で定義します。プロジェクション変換行列であれば、ディスプレイの縦横の比率(アスペクト比)や視野角などを定義できます。
そしてこれら三つの行列を掛け合わせて、最終的に出来上がった変換行列をシェーダに渡すわけですが、ここで一つ注意点があります。普通、一般的な数学の常識からすると、掛け算を行なう場合に掛ける順序は気にする必要がありませんよね。たとえば 2 x 3 は 6 ですし、3 x 2 も 6 です。しかし行列の場合には掛ける順序によって結果が変わります。行列というのは、そもそもそうした性質を元から持っているのです。ですから、モデル・ビュー・プロジェクションのそれぞれの行列を掛け合わせる順序には気を配らなくてはなりません。
実際にプログラムを組む段階になったらもう一度しっかり説明しますが、行列の掛け算には掛け合わせる順序が重要であるということだけは、覚えておきましょう。
まとめ
はい、かなりざっくりとした説明でしたが、なんとなく行列というものについて理解できたでしょうか。
今回のテキストは、あくまでも行列を理解するとっかかりでしかありません。途中でも少し書きましたが、行列を本格的に理解するためにはどっぷりと数学の世界に足を突っ込まなくてはいけなくなります。
3D レンダリングを行う上で、行列は欠かすことのできない存在です。そして、それを根本から理解するのは非常に大変です。ですから、あくまでも現時点では行列とはどんなものなのかをイメージできる程度で留めておいても、大きな問題はないと思います。
将来的には、もっと突っ込んだ行列の解説を行なう可能性はありますが、とりあえず、今はなんとなく行列というものを理解できていればそれでいいでしょう。大切なのは、行列の詳細な知識をゼロから理解することよりも、まずは使い方を知ることです。興味があれば、情報はウェブ上にたくさんありますし、理解が深まれば深まるほど有利であることは間違いありません。そこは自分自身の余裕に合わせて理解度を調節すればいいことです。
さて、次回はこれまた 3D を語る上では欠かせない存在である頂点とポリゴンについて解説します。
