反射光によるライティング

今回のサンプルの実行結果
様々なライティング
前回、前々回と、頂点シェーダによるライティングを解説してきました。
最初は平行光源によるライティング、すなわち拡散光によるライティングを解説しましたね。前回は拡散光によるライティングのデメリットである陰面(光の当たらない場所)の処理をカバーするため、環境光によるライティングを行ないました。
ライティング処理の三回目となる今回は、ここにさらに反射光(スペキュラライト)によるライティングを追加します。
反射光はその名の通り、光の反射をシミュレートします。概念としては平行光源による拡散光の概念と似ていますが、反射光を取り入れたレンダリングを行うことで、3D シーンはさらにリアリティを増します。
具体的には、反射光を取り入れることによってモデルに光沢や輝きを持たせることが可能になります。金属のような輝きのある面や、表面のツルツルした質感を表現するために反射光は非常に大きな役割を果たします。
ちなみにスペキュラ( specular )は、直訳すると[ 鏡面反射 ]・[ 鏡のような反射 ]といった意味になる言葉です。
反射光の概念
平行光源による拡散光のライティングでは、光の向き(ライトベクトル)と面の向き(面法線ベクトル)を用いて、その面がどの程度光を拡散させるのかを計算しライティングを行なっていましたね。光が最も強く当たっている場所はモデルの色がそのまま適用され、逆に光があまり当たっていない部分は暗い色になるようにプログラムを組みました。
しかし、金属のような質感、つまり光沢を表現するには拡散光だけでは不十分です。なぜなら、一番強く光が当たっている部分でも、せいぜいモデルの色がそのまま出るだけだからです。光沢を表すにはハイライトのような強い光を表現しなければなりません。
頂点シェーダをうまく修正すれば、拡散光だけでハイライトを入れることは不可能ではありません。しかし、大抵の場合それは微妙に不自然な結果になります。これは、拡散光が視線を考慮していないからです。拡散光は、何度も解説してきたとおり平行光源によるライティングで表現されますが、これは光の向きと面の向きだけを考慮したライティングです。反射光は、モデルを見つめる視線と光の向きとを考慮してライティングしますので、非常に自然なハイライトを表現できます。
視線を表すベクトルと、光の向きを表すベクトル、さらにここに面法線ベクトルを加えて計算を行うことで反射光の強さを算出できます。考え方としては、光源から放たれた光がモデルにぶつかって反射し、その反射した光と視線とがまっすぐに向き合っている場合に、最も強く光が視線に向かっていると言えます。下記の図のような感じですね。
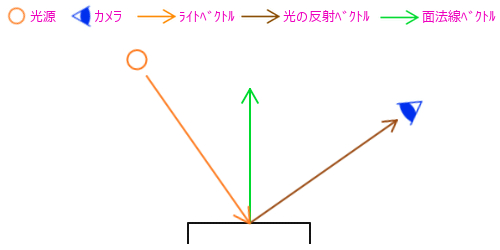
このような光の反射をそのままシミュレートすると、それなりに負荷の高い計算を行なわなくてはなりません。そこで、これと似たような結果を比較的軽い処理で得るための手法として、ライトベクトルと視線ベクトルとのハーフベクトルを使って反射光に近似した結果を求める方法があります。
ハーフベクトルを使う反射光の近似処理では、ライトベクトルと視線ベクトルからハーフベクトルをまずは算出します。そのハーフベクトルと面の法線ベクトルとの内積を取ることで反射光の強さを決定します。
面法線ベクトルとの内積を取るという処理は、以前にもどこかでやりましたね。
そう、平行光源による拡散光のライティングのときにも、ライトベクトルと面法線ベクトルとの内積を取りました。それとほとんど同じような処理の流れで、今度はハーフベクトルと面法線ベクトルとの内積を取ればいいのです。たったこれだけで、簡単に反射光を擬似的に表現することが可能になります。
頂点シェーダを修正する
さて、それでは早速コードを修正していきます。今回も前回までと同様に頂点シェーダ内で全ての計算を行い、最終的に算出された色情報をフラグメントシェーダに渡します。
頂点シェーダのソース
attribute vec3 position;
attribute vec3 normal;
attribute vec4 color;
uniform mat4 mvpMatrix;
uniform mat4 invMatrix;
uniform vec3 lightDirection;
uniform vec3 eyeDirection;
uniform vec4 ambientColor;
varying vec4 vColor;
void main(void){
vec3 invLight = normalize(invMatrix * vec4(lightDirection, 0.0)).xyz;
vec3 invEye = normalize(invMatrix * vec4(eyeDirection, 0.0)).xyz;
vec3 halfLE = normalize(invLight + invEye);
float diffuse = clamp(dot(normal, invLight), 0.0, 1.0);
float specular = pow(clamp(dot(normal, halfLE), 0.0, 1.0), 50.0);
vec4 light = color * vec4(vec3(diffuse), 1.0) + vec4(vec3(specular), 1.0);
vColor = light + ambientColor;
gl_Position = mvpMatrix * vec4(position, 1.0);
}今回新しく登場している attribute 変数はありません。視線ベクトルを表す eyeDirection が uniform 変数として追加されています。視線ベクトルは頂点ごとに異なる情報を表すものではなく、全ての頂点に対して一律で処理されるパラメータとして使われるので、 uniform 修飾子付きの変数として宣言するのですね。
平行光源による拡散光の処理と同様に、モデル座標変換行列の逆行列を使って視線ベクトルを変換します。その変換された視線ベクトルとライトベクトルとのハーフベクトルを変数 halfLE に取得しておき、これと面法線ベクトルとの内積を取ることで反射光を計算します。
しかしここで、初めて登場するビルトイン関数を使っているのがわかるでしょうか。
変数 specular に値を取得している部分で使っている pow というビルトイン関数がそれですね。この pow 関数は、べき乗を計算するための関数です。べき乗というのは 2 の 2 乗とか 3 乗とか、そういった計算のことですね。
反射光は強いハイライトを演出するためのものですので、内積によって得られた結果をべき乗によって収束させることで表現します。内積を取った結果は clamp 関数によって 0.0 ~ 1.0 の範囲に収まります。これをべき乗で処理すると、小さい数値はべき乗を重ねるたびにどんどん小さくなりますね。逆に、最も光の強い状態である 1.0 という数値は、何度べき乗を重ねても 1.0 のままです。※ 1 x 1 = 1 ですものね
反射光の計算ではべき乗をうまく活用することによって、弱い光をさらに弱く、強い光はそのまま残すという具合に変換させるのですね。こうすることで、ハイライトの特徴である強い光の反射効果を高めることができるのです。ちなみに、べき乗を行なう回数を減らすと、その分だけハイライトが広範囲に及ぶようになります。局所的な輝きであるハイライトらしさを演出するのであれば、ある程度の回数べき乗を行なうようにしたほうがいいでしょう。
また、反射光は光の強さを直接表す係数として使いますので、環境光と同じように加算処理で色成分に加えますので注意しましょう。それを踏まえると、最終的な色は次のような式で表すことができますね。
色 = 頂点色 * 拡散光 + 反射光 + 環境光
掛け算で処理するのは頂点色と拡散光だけであることに注意しましょう。
javascript を修正する
さて、続いてメインプログラムの修正です。
頂点シェーダでは若干複雑な修正を行ないましたが、javascript に加える修正はそれほど多くありません。要は uniform 変数として視線ベクトルを渡す処理を追加すればいいだけです。
uniformLocation を取得する処理
// uniformLocationを配列に取得
var uniLocation = new Array();
uniLocation[0] = gl.getUniformLocation(prg, 'mvpMatrix');
uniLocation[1] = gl.getUniformLocation(prg, 'invMatrix');
uniLocation[2] = gl.getUniformLocation(prg, 'lightDirection');
uniLocation[3] = gl.getUniformLocation(prg, 'eyeDirection');
uniLocation[4] = gl.getUniformLocation(prg, 'ambientColor');正しく uniformLocation が取得できたら、視線ベクトルを定義してからシェーダに送ります。基本的には、ビュー座標変換行列を生成する際に指定するカメラの座標を、そのまま視線ベクトルとして定義してやれば間違いありません。※カメラの注視点が原点の場合
視線ベクトルの定義と登録
// ビュー×プロジェクション座標変換行列
m.lookAt([0.0, 0.0, 20.0], [0, 0, 0], [0, 1, 0], vMatrix);
m.perspective(45, c.width / c.height, 0.1, 100, pMatrix);
m.multiply(pMatrix, vMatrix, tmpMatrix);
// 平行光源の向き
var lightDirection = [-0.5, 0.5, 0.5];
// 視点ベクトル
var eyeDirection = [0.0, 0.0, 20.0];
// 環境光の色
var ambientColor = [0.1, 0.1, 0.1, 1.0];
// (中略)
// uniform変数の登録
gl.uniformMatrix4fv(uniLocation[0], false, mvpMatrix);
gl.uniformMatrix4fv(uniLocation[1], false, invMatrix);
gl.uniform3fv(uniLocation[2], lightDirection);
gl.uniform3fv(uniLocation[3], eyeDirection);
gl.uniform4fv(uniLocation[4], ambientColor);視線ベクトルは三つの要素を持つ vec3 としてシェーダ内で使われますので、 uniform3fv でシェーダに送ります。今回のサンプルではライトベクトルと同様、視線ベクトルもずっと同じものが使われるので恒常ループのなかで処理しなくてもいいのですが、わかりやすさ重視でこのような感じになっています。
まとめ
さて、反射光について理解できたでしょうか。
計算のアルゴリズムはこれまでに行なってきたことと比べてそれほど難しくはないと思います。今回紹介した方法は、光源から放たれた光のベクトルと視線ベクトルとの間でハーフベクトルを算出し、面法線ベクトルと内積を取るだけなのでそれほど計算の負荷も大きくありません。ただ、あくまでも擬似的に反射光をシミュレートしているだけなので、真面目に光の反射を計算しているわけではありません。
レンダリング結果を見ると、それなりに綺麗にハイライトが入るのが確認できると思います。実際に動作するサンプルも下記のリンク先にありますので、参考にしてみてください。
次回は、グーローシェーディングとフォンシェーディングについて解説します。
