オブジェクトを行列で捻じるように変換

レイマーチングの行列処理

前回は行列処理を用いてオブジェクトを回転させてレンダリングする方法について解説しました。

行列に関する処理は得てしてわかりにくいものですが、回転だけに絞って考えてみるとそれほど複雑ではなかったのではないでしょうか。

今回のサンプルでも、前回と同様に行列を使います。とはいえ、今回は単なる回転ではなくレンダリングされるオブジェクトが捻じられたように変形するようにしてみましょう。見た目には結構面白いので、ぜひ挑戦してみてください。

行列を使った捻り

前回は行列を用いてオブジェクトの全体をまとめて回転させました。

ただ、勘のいい方であれば気が付いたと思いますが、実はオブジェクトを回転させる――という表現は実は正しくありません。これはコードの全体の流れがわかっていればおのずと思い浮かぶことだと思います。

どういうことかと言うと、distance function に渡される vec3 型のデータの実態がなんだったのか、思い出してみてください。

前回のサンプルのコードの一部

float distFunc(vec3 p){
	vec3 q = rotate(p, radians(time * 10.0), vec3(1.0, 0.5, 0.0));
	float d1 = distFuncTorus(q, vec2(1.5, 0.25));
	float d2 = distFuncBox(q);
	float d3 = distFuncCylinder(q, vec2(0.75, 0.25));
	return smoothMin(smoothMin(d1, d2, 16.0), d3, 16.0);
}

上記のコードは、前回のサンプルのコードを一部抜粋したものです。

この distFunc というユーザー定義関数の引数、 vec3 として入ってくるのはレイの先端座標でしたよね。

そうです、あくまでも座標変換されているのはレイのほうなんですね。

最終的なレンダリング結果だけを見ればオブジェクトが回転しているように見えますが、シェーダの中で加工されているのはレイ側の座標です。このことは前回までは触れてきませんでしたが、このあたりでしっかり認識しておきましょう。

そして、今回のテーマであるオブジェクトを捻じる座標変換ですが、こちらも先ほどの回転と同様に、実際にはレイの座標を変換してやることで結果的にオブジェクトを捻ったような感じでレンダリングさせます。

行列を用いて座標を変換するための、ユーザー定義の関数を今回も記述します。

該当するコードを見てみましょう。

捻じり変換関数

vec3 twist(vec3 p, float power){
	float s = sin(power * p.y);
	float c = cos(power * p.y);
	mat3 m = mat3(
		  c, 0.0,  -s,
		0.0, 1.0, 0.0,
		  s, 0.0,   c
	);
	return m * p;
}

前回の rotate 関数と同様に mat3 型の行列を使って座標を変換しているのが、パッと見ただけでもわかると思います。この関数は引数をふたつ、受け取るようになっています。

第一引数はレイの先端の座標、これはいつもと同じです。第二引数の power はその名の通り捻じる強さを決めるためのパラメータになります。

関数の中では、 power の値を使ってサインとコサインを求めていますね。ここをよく見てみると、引数として入ってきた power の値と、レイの Y 座標の値を使っているのがわかります。これがポイントです。

どうして Y 座標がポイントになるのかというと、その下の行列を生成している部分と関連してきます。

上記の抜粋コードのように、3x3 の行列の一番目、三番目、七番目、九番目にサインやコサインの値を指定する方法は、Y を軸とした回転を行う行列を生成するやり方です。前回解説した回転行列は、与えたパラメータによって X Y Z の各軸に対して回転を適用することができるものでした。今回の行列は、Y を軸とした回転だけを行うための行列なんですね。

レイの Y 座標の値を power の計算に使っているので、Y 座標の値次第で、当然捻じるための力の具合が変化します。そこに Y 軸回転を行う行列処理を加えることで、モデルの Y 座標の高低によって回転する度合いが変化、結果的に捻じれたようなレンダリング結果が得られるというわけです。

仮に、奥行き、あるいは横幅などを捻じりの係数として利用したければ、当然ですが行列の生成方法もそれに合わせる必要があります。

たとえば、X を軸とした回転を用いる場合であれば、次のようにすればいいでしょう。

捻じり変換 X 軸バージョン

vec3 twist(vec3 p, float power){
	float s = sin(power * p.x);
	float c = cos(power * p.x);
	mat3 m = mat3(
		1.0, 0.0, 0.0,
		0.0,   c,   s,
		0.0,  -s,   c
	);
	return m * p;
}

行列の中身が違う形になっているのがわかりますね。

同時に、捻じれ具合の計算に p.x が利用されているのも、見て取れるでしょう。要は、X 座標の値次第で、捻じれ具合が変化するようになるというわけです。

このような捻じり変換を利用すると、次のようなレンダリング結果となります。

X 軸捻じり

今回のサンプルで利用しているオブジェクトでは効果がわかりにくいですが、一応、Z 軸バージョンだと、次のような感じになりますね。

捻じり変換 Z 軸バージョン

vec3 twist(vec3 p, float power){
	float s = sin(power * p.z);
	float c = cos(power * p.z);
	mat3 m = mat3(
		  c,   s, 0.0,
		 -s,   c, 0.0,
		0.0, 0.0, 1.0
	);
	return m * p;
}

正しい結果を得るための注意点

さて、レイの座標変換を行って、オブジェクトを捻じった形でレンダリングする方法はわかりました。ただ、今回のサンプルの実行にあたっては注意すべき点がいくつかあります。

まず、今までのサンプルではなかなかそういった場面がなかったので触れてきませんでしたが、レイマーチング、とりわけ当サイトで扱ってきたようなスフィアトレーシングの技法では、状況によっては次の画像のように正しい結果が得られない場合があります。

まずはそのダメなパターンになってしまった場合を見てください。

失敗している例

これを見ると、何かがおかしいですね。

ちなみに描こうとしているオブジェクトの形状や個数は、冒頭に掲載したサンプルの実行結果画像と全く同じです。

失敗している例の場合、トーラスが途中でちぎれてしまっており、ドーナツのようにひとつながりになっていたはずの形が不自然に分断されてしまっています。

どうしてこのようなことが起こってしまうのでしょうか。

この問題の解決には、再度スフィアトレーシングの仕組みをきちんと理解する必要があります。

スフィアトレーシングでは、レイを段階的に伸ばしつつ、レイの先端とオブジェクトとの最短距離を指標に衝突判定を行っています。当然、レイの長さ次第ではオブジェクトの表面を突き抜けてしまうこともありますが、その場合にはレイの向きが反転することになるので、結果的にオブジェクトの表面に向かってレイの方向が反転し、レイの長さは徐々に収束していきます。

言葉ではなかなか伝わりにくいと思いますので、図解してみます。

オブジェクトを突き抜けてしまった場合の概念図

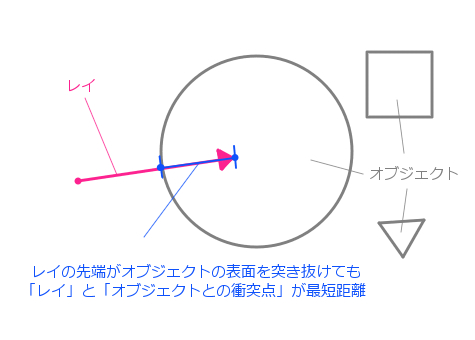
上記の図のような状況だと、ピンク色で表されるレイの先端が球体の表面を貫いて、内側に貫通してしまっています。しかし、青色で示している通り、レイの先端から最も近い場所にあるオブジェクトの表面は、レイが貫通してきた衝突点(レイとオブジェクト表面の交点)です。

このような場合は、マーチングループで次にレイが進む方向が反転することになります(上図でいうと右から左に進むレイに変わる)ので、結果的に衝突判定はうまくいきます。これなら、今まで通りの正しいレンダリング結果が得られます。

しかし、次のようなケースではどうでしょうか。

失敗する場合の概念図

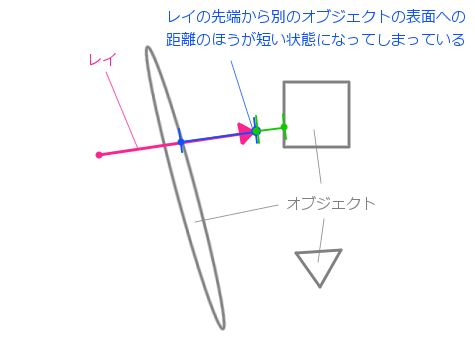
これを見るとわかるとおりオブジェクトが薄い構造をしている場合、レイの向きによってはオブジェクトを貫通してしまうことが考えられます。そして、貫通したその先の座標が奥にあるオブジェクトに近かったりすれば、当然スフィアトレーシングの仕組み上、最短距離にあるオブジェクトの方向にレイは進んでいきます。こうなると、手前にあるはずのオブジェクトは認識されなくなり、結果スクリーン上にレンダリングされなくなってしまいます。

また、極端に薄い構造になる部分など(それ以外でも状況によって起こる可能性はあります)では、まるで何もオブジェクトがない場所のようにレイが一直線に進み続けてしまう場合があります。要は、正しく衝突を検出できていない状態になってしまうわけです。当然、この場合は奥にオブジェクトがあればそれが見えてしまいますし、オブジェクトが何もなければいずれのオブジェクトとも衝突しなかったのと同じように背景がそのまま見えることになってしまいます。

これらのレイがオブジェクトを貫通してしまう問題は、マーチングループ内で、レイに長さを継ぎ足していく部分を修正してやれば解消できます。具体的には次のようにするのがもっとも簡単な解決法です。

マーチングループを修正する

float tmp, dist;
tmp = 0.0;
vec3 dPos = cPos;
for(int i = 0; i < 256; i++){
	dist = distFunc(dPos);
	tmp += dist;
	dPos = cPos + tmp * ray * 0.75; // 継ぎ足すレイを縮小
}

上記の例では、継ぎ足すレイの長さを 3/4 に縮小しています。この方法は手軽ですが、当然、一度に伸ばせるレイの長さが相対的に短くなるため、マーチングループの回数が少ないと別の問題を誘発することがあるので注意しましょう。

また、今回のようにオブジェクトに捻りを加えたりして、レンダリングされるオブジェクトが複雑な形状になる場合など、レイが貫通してしまう問題の他にも次のような症状が出ることがあります。

つぶつぶ症状問題

これを見ると、本来の色とは違うなにやらノイズのようなドット、あるいはラインが浮き出てしまっています。

これは法線を算出する際に結果が正しく取れていないことによるノイズです。ですから、法線に関する処理の一部を修正します。

法線算出の関数を修正

vec3 genNormal(vec3 p){
	float d = 0.001; // より広い範囲で勾配を計測する
	return normalize(vec3(
		distFunc(p + vec3(  d, 0.0, 0.0)) - distFunc(p + vec3( -d, 0.0, 0.0)),
		distFunc(p + vec3(0.0,   d, 0.0)) - distFunc(p + vec3(0.0,  -d, 0.0)),
		distFunc(p + vec3(0.0, 0.0,   d)) - distFunc(p + vec3(0.0, 0.0,  -d))
	));
}

前回までのサンプルでは、変数 d には 0.0001 を代入していました。この部分にほんの少し大きな値を設定してやることで、勾配の計測に利用される範囲が広がることになります。厳密過ぎる計算をすると先ほどのように逆にノイズが出てしまうこともあるわけです。このあたりは distance function との相性や、distance function の構造などにもよりますので、状況に応じて手動で調整するしかないような気もします。

まとめ

行列を用いてオブジェクトに捻りを加えてみましたが、いかがでしたか。

全体のコードは長くなるので載せませんが、前回のサンプルで distFunc 関数の中で rotate という自作関数を呼びだしていた部分を、今回は twist に変更してやればうまくいくはずです。

その他、ノイズの除去やレイの貫通対策など、少々細かなテクニックが登場しましたが、実際に自分で修正前と修正後を見比べてみるほうがいろいろとわかりやすいと思います。

レイマーチングではほんの小さな誤差がレンダリング結果に大きな影響を与える場合があります。逆に、今回紹介したノイズ除去のための法線計算のように、むしろ大雑把に大きな範囲で計算したほうが結果的にいいレンダリング結果が得られる場合もあったりします。このあたりは、経験値が高いほど、トラブルに対処する能力が高くなるような気がします。

まずは、自分でいろいろやってみる、そしてうまくいかない場合は理屈や原理から逆算して、なにをするべきか考え試してみる、これが大事かなと思います。

実際に動作するサンプルはいつものように以下のリンクから。

@h_doxas Twitter