MRT を利用した多重エッジ検出
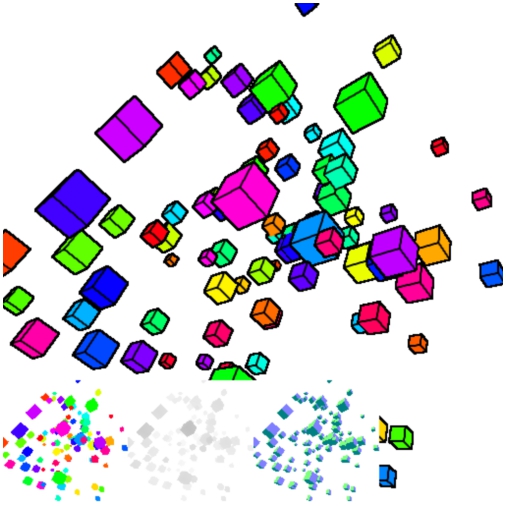
今回のサンプルの実行結果
異なるソースから正しいエッジ検出
前回は MRT と呼ばれる、複数のフレームバッファに同時に別々の情報を出力できる技術について扱いました。
MRT は WebGL 1.0 では拡張機能扱いですが、WebGL 2.0 では標準機能として普通に使えるようになる予定です。早い段階からしっかり MRT について知識を蓄えておくことで、いずれやってくる WebGL 2.0 時代を先取りしつつ、新しい技術を使いこなす基盤も作れるはずです。ぜひがんばって取り組んでみてください。
さて、今回はそんな MRT を利用したちょっと面白いテクニックを紹介します。
今回は、MRT を使って同時に複数のバッファに異なる情報を書き出し、それを利用してエッジ検出を行ってみましょう。
当サイトでは、これまでにも何度かエッジ検出自体は扱ってきました。エッジ検出の代表的な方法である sobel フィルタや laplacian フィルタがそれです。今回のサンプルでは、laplacian フィルタを用いてエッジ検出自体は行いますが、どんなレンダリング結果に対してエッジ検出フィルタを適用するのか、また MRT はどのように活用するのかなど、そのあたりに気をつけつつ読んでみるといいかもしれません。
そもそもどうしてエッジ検出に MRT?
今回のテーマはエッジ検出ですが、実際にエッジ検出が必要な場面とはどんなものが考えられるでしょうか。
大抵の場合、エッジ検出という言い方をした場合は、一度レンダリングした結果に対して二次元的に処理するポストエフェクトとして実装されます。エッジ検出を用いれば、たとえばモデルの輪郭線を表示して漫画やアニメのような雰囲気にしたり、あるいはエッジ検出した結果をぼかしてから、加算合成でレンダリング結果に加えることでぼんやりと光ったような演出を加えることもできたりします。このあたりは、発想次第というところがありますが、エッジ検出はその使い方によっては結構面白い効果を生む技術のひとつだと思います。
そしてここからが本題です。
なぜ、エッジ検出に MRT を利用するのか。これが今回のポイントでしょう。
今回実装するエッジ検出では、キューブのエッジ線を描画します。これは、冒頭のサンプル実行結果を見てもらえればわかると思いますが、キューブの一辺一辺がきれいに黒いラインで描かれています。これを正しく実現するために、MRT を使う必要が出てきます。
※MRT を利用しなくてもできますが、当然複数パスで実現することになります。
さて、ここで考えてみましょう。
次の図解で表しているキューブのエッジの内、一番目と二番目のそれぞれについて、どのような情報を元にエッジ検出をすればいいでしょうか。
異なるふたつのエッジ
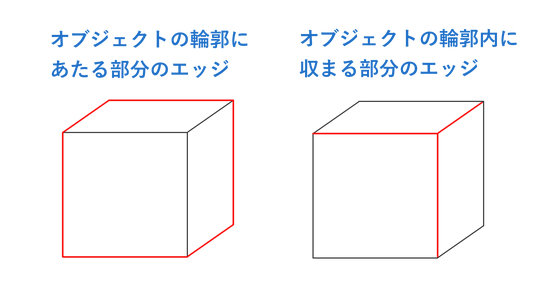
もしエッジ検出などをやったことがある方であれば、なんとなく想像がつくかもしれませんね。
まず、左側のオブジェクトそのものの外郭にあたるエッジを描画したければ、深度を用いて、各オブジェクトごとの重なりなどを調べてやれば、エッジの検出ができそうです。ほかにも、たとえばオブジェクトごとに固有のインデックスを振っておき、インデックスに応じて色をベタ塗りにしたシーンを用意しておけば、そこでエッジ検出を行うこともできますね。
一方の、右側のエッジ。これはどうすればいいでしょうか。
こちらは固有のインデックスを振るような方法では、全ての面が同じ扱いになってしまうためエッジは取れません。では深度で取ればいいかというと、深度もやはり緩やかに変化していくため、極端なエッジを検出するには役不足です。
答えを言ってしまうと、右側のエッジについては「法線」を使えばいいですね。各面はそれぞれ全く異なる方向に面が向いているので、法線情報を元にエッジを検出すれば、右側のエッジもしっかり取れそうです。
つまり、キューブのような角の立った形状の場合、外郭と内郭との両方をエッジとしてレンダリングしたい場合、最低でもふたつのリソースが必要になるわけです。そこで、従来ならそれぞれを別のフレームバッファに焼く手順で行う必要があった今回の要望を、MRT を使って一度にこなしてしまおうというわけです。
MRT を使ったエッジ検出、今回は深度と法線の二丁拳銃できっちり実現してみましょう。
ふたつのテクスチャへの同時書き出し
さて、それではまずは MRT を使ってふたつの異なる情報を別々のテクスチャへと書き出します。
これについては、流れは前回のサンプルとほとんど同じです。前回と異なっている点があるとすれば、前回は同時に4つの情報を MRT で書き出しましたが、今回は「色」と「深度」と「法線」の3つだけでいいという点でしょうか。
さっそくシェーダのソースを見てみましょう。
MRT シェーダ
// 頂点シェーダ
attribute vec3 position;
attribute vec3 normal;
attribute vec4 color;
uniform mat4 mvpMatrix;
uniform vec4 ambient;
varying vec4 vColor;
varying vec3 vNormal;
varying float vDepth;
void main(){
gl_Position = mvpMatrix * vec4(position, 1.0);
vColor = color * ambient;
vNormal = normal;
vDepth = gl_Position.z / gl_Position.w;
}
// フラグメントシェーダ
#extension GL_EXT_draw_buffers : require
precision mediump float;
varying vec4 vColor;
varying vec3 vNormal;
varying float vDepth;
void main(){
gl_FragData[0] = vColor;
gl_FragData[1] = vec4(vec3((vDepth + 1.0) / 2.0), 1.0);
gl_FragData[2] = vec4((vNormal + 1.0) / 2.0, 1.0);
}まず頂点シェーダのほうですが、今回はライティングを一切行わないため、非常に簡素な内容になっています。
MVP マトリックスで頂点座標を変換し、uniform 変数として送られてきた色を頂点カラーと合成して varying 変数に代入しています。法線は頂点情報をそのまま出力するのみ、深度については、前回とまったく同じロジックで計算しています。
フラグメントシェーダのほうも、ほとんど難しいことはやってないですね。varying 変数として入ってきた値を使って、MRT により複数のテクスチャに同時に出力しています。
上の内容を見ても、ほとんど前回と変わらないということがわかると思います。もしここで躓いてしまった場合は、多少面倒でも前回の内容からしっかり復習してみましょう。落ち着いて考えれば、特に難しいことはないはずです。
さて、上記のシェーダが走ると、フレームバッファにアタッチされた3つのテクスチャには、それぞれ頂点カラーベースのマテリアルの色、シーン全体の深度値、そしてモデルの法線情報の3つが個別に書きだされた状態になります。ここから、それぞれのテクスチャを同時に参照しながらエッジを検出していくわけですね。
エッジ検出シェーダの実装
エッジ検出には、前述のとおり laplacian フィルタを使いましょう。
詳細は以前当サイトで解説したテキストを見てもらうとして、具体的なシェーダの実装についてここからは見ていきます。
まずラプラシアンカーネルの情報は、javascript 側から uniform でシェーダに渡すようにしましょう。シェーダ内で動的に定義してもいいのですが、少しでもシェーダの負荷を下げるために、あらかじめ javascript で計算して渡してしまいます。
ラプラシアンカーネルとウェイトを javascript で定義
// カーネル参照のためのオフセット座標
var offsetCoord = [
-1.0, -1.0,
-1.0, 0.0,
-1.0, 1.0,
0.0, -1.0,
0.0, 0.0,
0.0, 1.0,
1.0, -1.0,
1.0, 0.0,
1.0, 1.0
];
// ラプラシアンカーネル
var weight = [
-1.0, -1.0, -1.0,
-1.0, 8.0, -1.0,
-1.0, -1.0, -1.0
];一応ざっくりとおさらいしておくと、ラプラシアンフィルタでは、参照しているテクセルの周囲をぐるっと囲むような8つの座標を参照しつつ、中心にあるテクセルの色と差分を取ります。中心の重みは 8.0 で、周囲が -1.0 です。つまり、中心の色と周囲の色がまったく同じ色である場合、全てを加算してやるとちょうどゼロになるという寸法ですね。逆に周囲の色が異なっていれば、当然値は 0.0 からどんどん離れていくということになります。
このラプラシアンフィルタのカーネルを使って、シェーダ内では深度と法線の両者からエッジを取ってやります。
今回の場合、周囲との色の差が大きければ大きいほど、エッジ検出したときに算出される値が 0.0 から遠い値になり、周囲との色の差がまったくない場合は、算出される値が 0.0 により近づいていく形になります。
そのことを踏まえたうえで、次のシェーダを見てみましょう。
マルチエッジ検出用のフラグメントシェーダ
precision mediump float;
uniform vec2 resolution;
uniform vec2 offsetCoord[9];
uniform float weight[9];
uniform sampler2D textureColor;
uniform sampler2D textureDepth;
uniform sampler2D textureNormal;
varying vec2 vTexCoord;
void main(){
vec2 offsetScale = 1.0 / resolution;
vec4 destColor = texture2D(textureColor, vTexCoord);
vec3 normalColor = vec3(0.0);
vec3 tmpColor = vec3(1.0);
float depthEdge = 0.0;
float normalEdge = 0.0;
for(int i = 0; i < 9; ++i){
vec2 offset = vTexCoord + offsetCoord[i] * offsetScale;
depthEdge += texture2D(textureDepth, offset).r * weight[i];
normalColor += texture2D(textureNormal, offset).rgb * weight[i];
}
normalEdge = dot(abs(normalColor), tmpColor) / 3.0;
if(abs(depthEdge) > 0.02){
depthEdge = 1.0;
}else{
depthEdge = 0.0;
}
float edge = (1.0 - depthEdge) * (1.0 - normalEdge);
gl_FragColor = vec4(destColor.rgb * edge, destColor.a);
}さて、ちょっと長いシェーダですが、上から順番に落ち着いて見ていきましょう。
まず大前提として、uniform 変数のそれぞれの意味をしっかり理解しておきましょう。
uniform 変数の意味
uniform vec2 resolution; // テクスチャの解像度
uniform vec2 offsetCoord[9]; // オフセット参照するテクスチャの座標
uniform float weight[9]; // ラプラシアンカーネルのウェイト
uniform sampler2D textureColor; // 頂点カラーテクスチャ
uniform sampler2D textureDepth; // 深度テクスチャ
uniform sampler2D textureNormal; // 法線テクスチャ各種 uniform 変数のうち resolution はフレームバッファを初期化した際の幅と高さですね。今回のサンプルでは 512px の正方形です。
続いて出てくる offsetCoord と weight はいずれも javascript 側で定義したものです。配列としてデータを受け取るようになっています。
あとは、前述の MRT シェーダでそれぞれ書き込んだ情報をテクスチャとして渡している感じですね。
続いて main 関数の中身を見ていきます。
ここではいくつかの変数を初期化すると共に、ループ処理を行いながらラプラシアンカーネルを用いた計算を行っています。
ポイントは、uniform 変数の中身をちゃんとイメージしながら一連の処理を眺めてみることでしょう。
まずシェーダの冒頭で offsetScale という変数に、テクスチャの解像度の情報を使って何かを計算していますね。
解像度からオフセットする量を算出
vec2 offsetScale = 1.0 / resolution;GLSL では、テクスチャの参照にはテクスチャ座標を用いますね。このテクスチャ座標は原則 0.0 から 1.0 の範囲なので、厳密に 1 テクセルだけとなりの座標を見に行く……といったことがやりたい場合、解像度を元に 1 テクセル分のオフセット量をあらかじめ算出しておく必要があります。ここはそのための処理ですね。
さらにその下では、変数名に Color というキーワードが入った変数を3つ定義しています。
ここも一見すると何をしているのかわかりにくいかもしれませんが、まず最初の destColor には、頂点カラーとマテリアルの色を出力したテクスチャから、普通に色を読みだして入れておきます。このとき取得した色に、エッジ検出の結果を最終的に掛け合わせることになります。
その他の normalColor と tmpColor には、それぞれ初期値として 0.0 と 1.0 を代入しておきます。これはまたあとで出てきます。
さらにその下、今度は Edge というキーワード付きの変数がふたつあります。これは、エッジの検出された結果を格納するための変数です。
法線で算出したエッジと、深度で算出したエッジ、それぞれを格納するためにふたつ用意している感じですね。
さて、次に出てくるのがラプラシアンカーネルを使って色の差分を計算するためのループ処理です。
色の差分を算出するためのループ処理
for(int i = 0; i < 9; ++i){
vec2 offset = vTexCoord + offsetCoord[i] * offsetScale;
depthEdge += texture2D(textureDepth, offset).r * weight[i];
normalColor += texture2D(textureNormal, offset).rgb * weight[i];
}
normalEdge = dot(abs(normalColor), tmpColor) / 3.0;ここではオフセットする量分だけ移動した座標をまず作り、それを使ってテクスチャを参照します。
参照した結果は、ラプラシアンカーネルのウェイトを掛けてやりつつ、すべて加算していきます。深度値については、テクスチャを参照して取得できる色は当然ながら RGB ですが、実際には白黒のレンダリング結果になっているので R の値だけを使えばいいですね。
一方で法線については RGB がそれぞれ異なる結果になっているので、直接 Edge として取るのではなく一度 RGB のカラーとして変数に加算していきます。
最後のところでやっている計算がちょっとわかりにくいかもしれませんが、ここは落ち着いて考えてみましょう。
まず normalColor の RGB の各要素には、ラプラシアンカーネルを使った計算結果の加算された値が入っているので、場合によってはマイナスの数値が入っている可能性があります。そのため abs 関数を使って絶対値を取るようにしています。さらに、その絶対値を取ったあとの法線と、ループ構造の前に定義しておいた tmpColor で内積を取っていますね。
これは、内積の計算方法がベクトルの各要素を掛けたあと全て加算するという処理であることを考えてみれば、何がしたいのかわかりやすいのではないでしょうか。
法線に対してラプラシアンカーネルで計算した結果は、当然ながら RGB が個別に算出されます。R 成分的にはほとんど同じでも、G や B は差分が大きいなんてケースも考えられますね。そこで、絶対値を取った RGB の各要素を全て加算して 3.0 で割るような処理をしたいわけですね。
この場合、もちろん次のように書いても間違いではありませんが、今回の場合はまったく同じ処理を行うことができる一行のコードとして、内積を使った書き方をしているのですね。
両者は同じ意味
// 今回のサンプルのコード
normalEdge = dot(abs(normalColor), tmpColor) / 3.0;
// 以下でも意味は同じ
normalEdge += abs(normalColor.r);
normalEdge += abs(normalColor.g);
normalEdge += abs(normalColor.b);
normalEdge /= 3.0;変数の初期化を行っている部分で tmpColor というよくわからない変数を用意して、中身を 1.0 で初期化していたのは、こうして内積により簡潔に記述するためだったんですね。ただしこれは気持ちの問題というところもあるので、上記のように三行でしっかり書いたほうがむしろ簡潔だ! と感じる場合には無理して省略しなくてもいいと思います。
深度のエッジを二値化
さて、法線からのエッジ検出はできました。
深度についても、先ほどのループ構造でエッジ検出自体はできているのですが、今回のようなやり方の場合、深度の差が大きくないと、あまり強烈なエッジとしてラインが出てきません。少ししか深度に差のない部分では、そのままだと薄い線になってしまうわけです。
そこで今回は一度条件分岐を使って値をチェックしてやり、一定以上の深度値の差がある場合には極端にエッジが出るように強制しています。
該当箇所を抜粋
if(abs(depthEdge) > 0.02){
depthEdge = 1.0;
}else{
depthEdge = 0.0;
}ここで唐突に比較対象として使っている 0.02 という値は目算で調整しました。あまり大きな値にし過ぎると全然エッジが出なくなってしまいますし、あまり小さな値にするとちょっとした傾斜などでも不自然にエッジが描かれたりしてしまいます。
今回は浮動小数点テクスチャなどのような、精度の高いテクスチャフォーマットを使っていないのでこのような応急処置を施しました。それでも、見た目としてはそこそこ綺麗に仕上がっているのではないかなと思います。
シェーダではそれ以降、検出したエッジの値を深度と法線とを加味したものに再計算したあと、マテリアルの色に乗算して最終的な結果として出力しています。ベタ塗りのキューブの色しか無かった部分に、しっかりとエッジの線が出るようになったはずです。
まとめ
さて、最後にまとめとして再度、どうして深度と法線とのダブルエッジ検出が必要なのか考えてみましょう。
たとえば、深度だけのエッジ検出を行った場合はどうでしょうか。この場合、内郭のエッジの線がうまく検出できません。しかしそれなら、法線だけでエッジ検出してもイイんじゃないの? と思うかもしれません。
しかし、法線だけでエッジを取ると、偶然同じ法線同士の面が前後に並んだ場合に、うまくエッジが取れなくなります。
同じ法線を持つ面が重なってもエッジが取れている
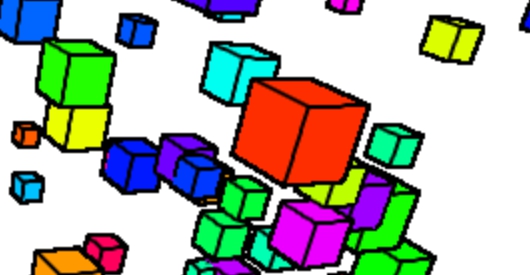
上の画像の、ちょうど中心あたりにある赤いキューブに注目してみてください。
右側を向いている面は、その奥にある黄緑色のキューブの同じ方向にある面と重なっている箇所がありますね。
もし仮に、法線だけでエッジを検出していると、このように同じ法線を持つ面同士が重なった場合、正しくエッジが取れなくなります。しかし、今回の場合はここに深度の情報もプラスして考えるようにしているため、正しくエッジが取れているわけですね。
エッジ検出をより完全なものにしたければ、たとえばマテリアルの色に対してもエッジの検出を行うようにしてやれば、座標と法線とが非常に近しいという稀なケースに対しても完璧にエッジを取ることができます。今回はダブルエッジ検出でしたが、負荷に対してそれほどデリケートにならなくてもいい場合は、マテリアルやインデックスを使ったより精度の高いエッジ検出を実装してみるのもいいかもしれません。
エッジを描いてやることによって、アニメのような独特な雰囲気のシーンがレンダリングできます。今回はあまり javascript 側の実装について触れていませんが、詳細はサンプルのコードや、前回のテキストの内容をしっかり見てみれば理解できる範囲だと思います。
今回も、サンプルは以下のリンクから参照できます。
