半球ライティング

今回のサンプルの実行結果
自然な照り返し
前回はステンシルバッファを用いた鏡面反射を扱いました。
[ あえて描かない技術 ]であるステンシルバッファを用いることで、鏡面となる板ポリゴンからはみ出してしまう領域を切り抜き、自然なレンダリングが行なえるのでしたね。ステンシルバッファは使いどころが難しいバッファですが、こんな活用方法もあるのだなと感じていただけたら幸いです。
さて、今回は半球ライティング(hemisphere lighting)です。そんなに難しいテクニックでもないので今更感はありますが、やってみましょう。
半球ライティングはその名のとおり、三次元空間上を一つの球に見立ててライティングを行なう技術です。以前に解説した環境光によるライティングをより発展させたような効果が得られます。
環境光(アンビエント)による照明効果は、ライトが当たっていない部分に趣を持たせます。モデル全体にうっすらと照明効果を持たせることで、平行光源によるライティングが行なわれない領域の不自然さを緩和します。
たとえば現実世界の晴れた日などでは、太陽から直接降り注ぐ光が平行光源と同じように物体を照らします。しかし実際には、太陽から放たれた光はあらゆる物体にぶつかり反射し、モデルにぶつかります。床や地面に一度ぶつかった光が、乱反射を繰り返して物体にあたることで直接光が当たらない部分も微妙に明るくなるわけです。この現象を再現しているのが、環境光によるライティングでしたね。
今回の半球ライティングはこれをさらに発展させたものです。光の乱反射を再現する際に、上空の方に向いている面は空の色に、地面の方を向いている面は地面の色にそれぞれ塗り分けます。上空と地面、二つの領域を球体の上部と下部に半々にして考えるために半球ライティングという名前がついているのですね。
半球ライティングの考え方
先述の通り、半球ライティングでは天空と地面、二つの領域を球体の上部と下部にわけて考えます。
モデルの面の向きは、頂点法線を使って表すことができますね。球体の地面の向きは、天空方向がわかれば同様にベクトルで表すことができます。
法線と天空方向
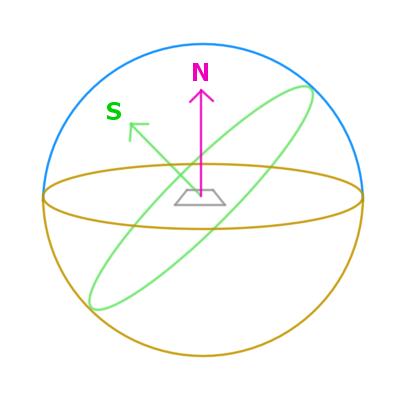
上の図では、球体の中にグレーの線で板状のモデルがあると仮定しています。そのモデルの法線方向を表しているのがピンク色の矢印で描かれている N です。一方、地面の向き、つまり天空方向は緑色の矢印で描かれている S になります。
今回のサンプルでは、地面は Z 軸から見て平行な面として作成しますので、上の画像とはちょっと違ってしまいますが S は上に向かってまっすぐ伸びるベクトルになります。傾斜した地面(坂道など)の場合は、当然ですが地面からの照り返しも地面の向きによって変わってきます。つまり S は地面のそのときそのときの向きに合わせて適宜変えてやればいいわけですね。
照明色の導き方
半球ライティングでは、空の色と地面の色という二つの色を使って、最終的な環境光の色を決定します。
今回のサンプルでは、空の色は純粋に青です。地面の色は茶色っぽい色にしてあります。天空色と地面色、この二つを先ほどの N と S を使って線形合成した結果が、最終的な環境光の色になります。
最終的な色を導き出すためには、以下のような式を用います。
半球ライティングの式
天空色 * Cosθ + 地面色 * -Cosθここで登場するθは、先ほどの N と S のなす角です。Cosθは内積を使うことで求めることができますが、上記の式のとおりに計算すると、当然と言えば当然ですが結果は -1.0 ~ 1.0 という範囲を取ります。色を表す場合にはマイナスの値があると困ってしまうので、この結果を正規化して 0.0 ~ 1.0 の範囲に収まるようにしてやることで、半球ライティングが行なえそうです。
結果を正規化するには、先ほどの計算結果に 1.0 を足した上で、それを半分にしてやればいいですね。これを踏まえると、式を以下のように変換してやればよさそうです。
正規化式
((天空色 * Cosθ + 地面色 * -Cosθ) + 1.0) * 0.5上記の式をシェーダ内で計算することができれば、半球ライティングが実現できます。
シェーダの実装
それではここまでの内容を踏まえてシェーダを記述していきましょう。
まず今回のサンプルでは、いくつか新しい要素をシェーダに送る必要があるものの、基本的には単純なライティングとさほど変わらないということを覚えておきましょう。つまり、今まで解説してきたテクニックを使いまわすだけで、半球ライティングは比較的簡単に実現できます。
通常の平行光源によるライティングと異なる点は、ライトベクトルのほかに地面の向きを表すベクトル、つまり天空方向を示すベクトルが必要になることがまず一点。そして今まではアンビエントカラーとしてシェーダに送っていた色情報を、天空色と地面色の二つに分けて送ってやります。
半球ライティングのシェーダソース
// 頂点シェーダ
attribute vec3 position;
attribute vec3 normal;
attribute vec4 color;
uniform mat4 mMatrix;
uniform mat4 mvpMatrix;
uniform mat4 invMatrix;
uniform vec3 skyDirection;
uniform vec3 lightDirection;
uniform vec3 eyePosition;
uniform vec4 skyColor;
uniform vec4 groundColor;
varying vec4 vColor;
void main(void){
vec3 invSky = normalize(invMatrix * vec4(skyDirection, 0.0)).xyz;
vec3 invLight = normalize(invMatrix * vec4(lightDirection, 0.0)).xyz;
vec3 invEye = normalize(invMatrix * vec4(eyePosition, 0.0)).xyz;
vec3 halfLE = normalize(invLight + invEye);
float diffuse = clamp(dot(normal, invLight), 0.1, 1.0);
float specular = pow(clamp(dot(normal, halfLE), 0.0, 1.0), 50.0);
float hemisphere = (dot(normal, invSky) + 1.0) * 0.5;
vec4 ambient = mix(groundColor, skyColor, hemisphere);
vColor = color * vec4(vec3(diffuse), 1.0) + vec4(vec3(specular), 1.0) + ambient;
gl_Position = mvpMatrix * vec4(position, 1.0);
}
// フラグメントシェーダ
precision mediump float;
varying vec4 vColor;
void main(void){
gl_FragColor = vColor;
}今回のサンプルでは、色の計算は全て頂点シェーダ側で行なうようにしています。フラグメントシェーダは、頂点シェーダから送られてきた色情報をただ出力しているだけですね。
ライトベクトルを使ってディフューズカラーやスペキュラーカラーを求めているところは今までと全く一緒です。ポイントは頂点シェーダの main 関数の中で登場する以下のコード。
main 関数内の処理
float hemisphere = (dot(normal, invSky) + 1.0) * 0.5;
vec4 ambient = mix(groundColor, skyColor, hemisphere);ここで登場する invSky は逆行列を適用した天空方向を表すベクトルです。このベクトル(S)と法線(N)との内積を取り、先ほどの式と同じように 1.0 を足して半分にしたものが、色の線形合成に使われる係数になります。色を線形合成するにはシェーダの組み込み関数 mix を使えば簡単です。ここで得られた色をアンビエントカラーとしてモデルに適用してやるわけですね。
javascript 側のメインプログラムでは、シェーダへ正しくデータをプッシュしてやるだけで、今までのサンプルと比べて特別なことはやっていません。ここまで順にテキストを読み進めてきた方なら問題なく理解できると思います。
まとめ
さて、半球ライティング、いかがでしたでしょうか。
概念はそれほど難しくなく、シェーダの記述も今までとそれほど変わりません。計算の負荷も通常のライティングと比較してさほど重いということもないと思いますし、リアルな環境光による効果を得るには、非常に効果的な手段の一つなのではないでしょうか。
屋外のシーンをレンダリングする場合に限らず、屋内のシーンでも光源が複数あるような場合には、半球ライティングを応用することでそれほど負荷をかけずにリアルなシーンがレンダリングできそうです。状況に応じて、使ってみてはいかがでしょうか。
今回のサンプルも実際に動作するものを見たい場合には以下にリンクがあります。
