オブジェクトの複製 repetition
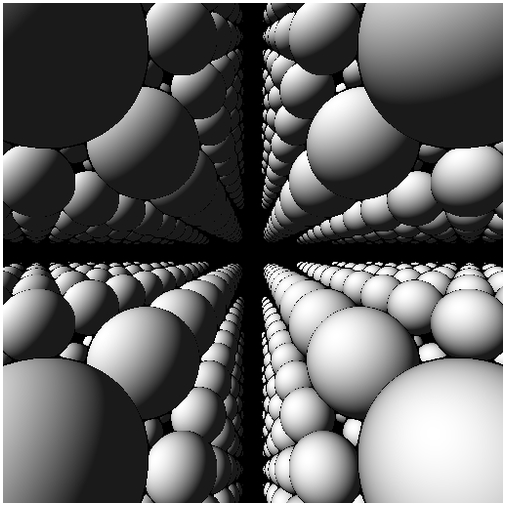
今回のサンプルの実行結果
ray marching repetition
前回は視野角を考慮しつつ、任意の三次元空間を切り取るためのレイの定義について解説しました。
視野角の概念を理解していると、レンダリングの対象となるシーンを操作することがしやすくなります。必ずしも前回紹介したようなレイの定義を用いることが正解ではないにせよ、様々な状況に対応できるように基礎を磨いておくことは無駄にはなりません。
少々難しい数学の話に感じたかもしれませんが、レイマーチングを本格的にやっていく上では前回の内容は初歩の初歩です。最初は難しく感じるかもしれませんが、諦めずにがんばってください。
さて、今回は掲題のとおり repetition について解説します。要は、オブジェクトを複製してレンダリングするテクニックについてです。
冒頭のサンプル実行結果のキャプチャ画像を見るとわかると思いますが、今回紹介するテクニックを用いると同じ形状のオブジェクトを一度に複製して大量にレンダリングすることが可能になります。レンダリング結果だけを見ると、すごく難しい技術を使うのではと心配になるかもしれませんが、distance function にほんの少しのエッセンスを加えるだけで割と簡単に実現できます。
事実、シェーダに追加するコードはほんのわずかです。それこそ、拍子抜けしてしまうほどに。
重要なのは、どうしてそのわずかなコードを追加しただけで、レンダリング結果が劇的に変化するのか、その仕組みを正しく理解することです。
distance function と repetition
repetition という単語を直訳すると、その意味は[ 反復 ]や、[ 繰り返し ]です。そのままの意味ですね。
先ほども書いたとおり、レイマーチングではシェーダにひと工夫するだけで、同一形状のオブジェクトを大量に複製することができます。出し惜しみしても仕方ないので、ここはまずシェーダのコードから見てみましょう。
フラグメントシェーダのコード
precision mediump float;
uniform float time;
uniform vec2 mouse;
uniform vec2 resolution;
const float PI = 3.14159265;
const float angle = 60.0;
const float fov = angle * 0.5 * PI / 180.0;
vec3 cPos = vec3(0.0, 0.0, 2.0);
const float sphereSize = 1.0;
const vec3 lightDir = vec3(-0.577, 0.577, 0.577);
vec3 trans(vec3 p){
return mod(p, 4.0) - 2.0;
}
float distanceFunc(vec3 p){
return length(trans(p)) - sphereSize;
}
vec3 getNormal(vec3 p){
float d = 0.0001;
return normalize(vec3(
distanceFunc(p + vec3( d, 0.0, 0.0)) - distanceFunc(p + vec3( -d, 0.0, 0.0)),
distanceFunc(p + vec3(0.0, d, 0.0)) - distanceFunc(p + vec3(0.0, -d, 0.0)),
distanceFunc(p + vec3(0.0, 0.0, d)) - distanceFunc(p + vec3(0.0, 0.0, -d))
));
}
void main(void){
// fragment position
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, resolution.y);
// ray
vec3 ray = normalize(vec3(sin(fov) * p.x, sin(fov) * p.y, -cos(fov)));
// marching loop
float distance = 0.0;
float rLen = 0.0;
vec3 rPos = cPos;
for(int i = 0; i < 64; i++){
distance = distanceFunc(rPos);
rLen += distance;
rPos = cPos + ray * rLen;
}
// hit check
if(abs(distance) < 0.001){
vec3 normal = getNormal(rPos);
float diff = clamp(dot(lightDir, normal), 0.1, 1.0);
gl_FragColor = vec4(vec3(diff), 1.0);
}else{
gl_FragColor = vec4(vec3(0.0), 1.0);
}
}一度にズラッとコードを見せられても、どこに修正が加えられたのかわかりにくいと思いますが、注目すべきは distance function を定義しているあたりのコード。
前回までのサンプルでは、distance function のなかで length には引数として受け取った座標をそのまま渡していました。ところが、今回はそこがちょっと変わっていますね。なにやら怪しげな trans という関数が呼び出されていることがわかると思います。
この trans 関数は、GLSL のビルトインなどではありません。
distance function の定義されている上を見ると、そこに trans 関数の定義が書かれているのがわかるでしょう。わかりやすいように以下抜粋します。
trans 関数
vec3 trans(vec3 p){
return mod(p, 4.0) - 2.0;
}さて、これを見ると trans 関数はかなり簡易な構造になっていることがわかります。 vec3 型の引数をひとつ受け取り、何かしらの計算を行ってそのまま返していますね。
この関数のなかで登場している mod は今までに何度も出てきていますし、他の言語などでも割とよく見かけるので説明は不要かと思います。要は、除算の剰余を求めるためのビルトイン関数ですね。 trans 関数は、引数として受け取った座標の情報を、その mod に渡しているだけです。どうしてこれで、オブジェクトの複製ができるのでしょうか。それに、なぜ 4.0 で除算した余りから 2.0 を引いているのでしょう。
次項より詳しく見ていきましょう。
mod を利用して repetition
数学的なことを考えるときは、個人的には何事もすごく単純化して考えるようにしています。そこが足がかりとなって、全容が把握できてくることも多いように思うからです。
今回の場合も、コードを vec3 の座標として考えるのではなく、シンプルに X の要素にだけ絞って考えてみましょう。
カメラから放射状にレイが伸びるとき、カメラから遠ざかれば遠ざかるほど、当然 X の値は 0 から離れた数値になっていきますね。これは図解してみればすぐにわかると思います。
シーンを上から眺めた図
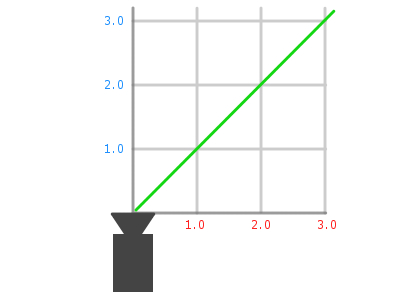
正負の違いはあるにせよ、シーンの奥に行けば行くほど X の値はどんどん 0 から離れて大きくなるか小さくなるかしていくわけです。たとえば、上の図で Z が 3.0 の場合のときを考えてみると、緑色で表わされているレイの X 座標の値は 3.0 になるはずです。ここまでは簡単ですね。そして、この X = 3.0 という状態で仮に mod(X, 2.0) による計算が行われるとどうなるでしょうか。
この場合だと、3.0 を 2.0 で割ったその余りですから、答えは 1.0 になりますね。同様に考えると、もし X の中に 5.0 という座標が入っていた場合でも、計算結果はやっぱり 1.0 です。仮に X がもっと大きな値だったとしても、解は必ず 0.0 ~ 1.99999…… の範囲に収まるはずです。簡単ですね。
さて、ここで再度 trans 関数のコードを見てみます。
trans 関数
vec3 trans(vec3 p){
return mod(p, 4.0) - 2.0;
}これを見るとわかるとおり、 mod には引数として入ってきた座標と 4.0 が指定されています。このことから、引数の p の中身がどのような座標であったとしても、それぞれ 0.0 ~ 3.99999…… の範囲にクランプされてしまうことがわかります。 trans 関数の正体は、要するにレイの座標情報をクランプしてしまう関数という、ただそれだけだったんですね。
最終的には除算した剰余から、除算に用いた値のちょうど半分の値を減算してから返します。これは mod の計算結果を 0 を中心とした正負の方向に振り分けるためです。たとえば今回のサンプルの場合なら 0.0 ~ 3.99999…… という範囲を -2.0 ~ 1.99999…… という範囲になるようにオフセットさせるわけですね。
このように、distance function に渡された座標情報を一定の範囲にクランプすることによって、特定の範囲の値が反復するような状態を作ることができます。これにより、スクリーン上には大量のオブジェクトがレンダリングされることになるのですね。
repetition を利用する際の注意点
さて、反復して複数のオブジェクトが描かれる仕組みは理解できたでしょうか。
先ほどはわかりやすく説明するために X に限定して考えましたが、実際にはこれが X Y Z の各軸に対して起こります。※もちろん mod に与えるデータや戻り値を工夫すれば、特定の座標軸に対してだけ計算を適用することもできます
repetition を利用する上では、いくつか注意しておくべきポイントがあります。
まず、基本的に今回のような repetition は等間隔でオブジェクトが描かれます。これは先ほど説明した仕組みがわかっていれば理解できると思います。ランダムにいくつものオブジェクトを配置するような処理には、今回の方法は適していません。
また、原則としてオブジェクトは無限遠に複製されていきます。一定の範囲だけに限定してオブジェクトを配置したければそれなりに工夫が必要になるでしょう。
それと、もうひとつ大事なポイントがあります。今回シェーダに追加したコードは非常に少ないコードだけですが、前回のサンプルと比較して、実はこっそりと修正されている箇所があったことに気がついたでしょうか。
その修正箇所とはマーチングループを行っている部分のコードです。
該当箇所のみを抜粋
for(int i = 0; i < 64; i++){
distance = distanceFunc(rPos);
rLen += distance;
rPos = cPos + ray * rLen;
}前回までは、マーチングループを 16 回ループさせていました。今回は、このループ回数が 4 倍の 64 回になっています。ちょっと不思議に思うかもしれませんが、まずはループ回数をそのまま 16 回にしていた場合のレンダリング結果を見てみてください。
ループ回数 16 の場合

オブジェクトの複製自体はうまくいっている気配がしますが、一方でほとんどの球体が不完全な形状になってしまっていることがわかりますね。
これは、レイマーチング(スフィアトレーシング)の仕組みを思い出してみれば原因がわかるはずです。
スフィアトレーシングでは、レイを段階的に伸ばしていきます。そして、そのレイを伸ばす単位はオブジェクトとの最短距離でしたよね。つまり、レイが直接オブジェクトに衝突しなくても、オブジェクトに近い距離を通っている場合にはなかなかレイが伸びていかないことになってしまいます。
今回のように repetition を用いる場合に限りませんが、シーンの中にオブジェクトが大量にある場合、当然ながらオブジェクトすれすれの位置を通過していくレイは比例して増えていきます。つまり、レイの方向とオブジェクトの位置関係次第で、あまり長さの伸びないレイが出てくるわけです。
こういった場合、マーチングループの回数が十分に多くないと、非常に短い距離までしかレイが到達しない場面が出てきます。先ほどのループ回数 16 回のレンダリング結果は、まさにそれが起こっているのですね。手前にある球体の淵に近い部分は、黒く塗り潰されてしまっているのがわかると思います。この部分のレイは、奥の球体に衝突するまで伸びきらなかったわけです。
そこで、ループ回数を増やして 64 回にしてやると以下のようになります。
ループ回数 64 の場合

今度はしっかりとレンダリングされているように見えますね。
それでも、よく見てみると奥に行くと途中で球体のレンダリングがされなくなってしまっているのがわかります。先ほども書いたように mod を使った今回のようなオブジェクトの複製方法では、理論上は無限に球体が連続して描かれていなければいけないはずです。しかし、64 回ループさせても到達できない部分の描画はやはり行われないのです。
このように、オブジェクトを複製させたり、あるいは大量のオブジェクトをシーン中に描かなければならない場合など、どうしてもマーチングループの回数を増やしてやる必要が出てきます。各ピクセルに対して処理を行うフラグメントシェーダ内でループするだけでも、いかにも負荷が高い処理であることは容易に想像できます。つまり、レイマーチングにおいてはこのループ回数とレンダリング結果の品質とは常にトレードオフの関係にあるのです。
まとめ
さて、repetition と呼ばれるオブジェクトの複製について、理解できましたでしょうか。
オブジェクトを複製できると言っても、等間隔にしか配置できなかったり、場合によっては高負荷な処理になってしまうことがあるなど、少々使いどころの難しい repetition。しかし、見た目のインパクトは割と強いと思いますし、応用テクニックとして覚えておくといいでしょう。
mod は比較的いろんな場面で利用できる便利な関数です。repetition を通してその扱い方の基本を身につけておきましょう。
実際に動作するサンプルはいつものように以下のリンクから。
