レイマーチングで球体を描く

今回のサンプルの実行結果
ray marching に挑戦しよう
前回は GLSL 内でレイを定義する方法について解説しました。
レイマーチングにしてもレイトレーシングにしても、まずはシェーダ内で扱うレイを定義しないことには次に進めません。前回の内容は普段から数学に馴染みのない方にはちょっと難しい部分もあったかもしれませんが、すべての基本となる部分ですのでしっかりと理解できるようにがんばってください。
さて、今回ですが、いよいよ実際にレイマーチングの枠組みとなる部分のコードを記述して、GLSL だけで球体をレンダリングしてみます。
とは言っても、冒頭のサンプル実行結果を見てもらえれば一目瞭然かと思いますが、今回のサンプルでは黒い画面上に白く型を抜いたように円が描かれるだけです。今回の内容も、前回同様に非常に基本的な部分であり派手さはまったくと言っていいほどありません。しかし、レイマーチングで球体をスクリーン上に描き出すことは間違いなくできるようになります。
何事も基本は大事です。目にした人をあっと驚かせるようなレイマーチングの実装を習得するためにも、今回の内容をぜひしっかりと理解してください。
distance function
前回のテキストで解説したように、レイマーチングの手法のひとつであるスフィアトレーシングでは段階的にレイを伸ばしていきオブジェクトを認識します。
これは図解して解説しましたね。
レイマーチングの概念図
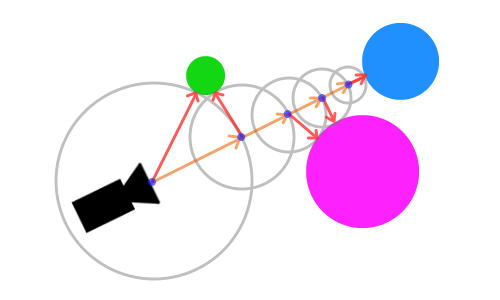
レイの原点からオブジェクトまでの最短距離を算出し、それと同じ距離の分だけレイを伸ばしていくのでしたね。
レイマーチングでは、この最短距離を算出するための仕組みとして distance function を用います。distance は直訳して[ 距離 ]です。その名前からも、最短距離を算出するための関数であることが想像できると思います。
distance function は、function とついていることからもわかるとおり、引数としてパラメータを受け取って何かしらのデータを返すような関数として記述します。では、この distance function が返すデータとはいったいなんなのか? これは簡単ですよね。
そう、distance function が返すのは、オブジェクトまでの最短距離です。
GLSL でレイマーチングの実装を行う場合、この distance function の設計が非常に重要になります。具体的には、引数としてレイの原点座標を受け取り、そこから最も近い場所にあるオブジェクトまでの距離を返すような関数を作るわけです。
しかし、ここまで読み進めてきても、大半の人は嫌な予感しかしないと思います。3D プログラミングには行列や四元数など、非常に難解な数学の問題がよく登場しますね。オブジェクトまでの最短距離を返す関数なんて、きっと恐ろしく複雑なコードなんじゃないの――と考えるのが普通だと思います。
しかし、心配する必要はありません。
実は、distance function は比較的シンプルに記述できることが多いです。概念が少々難しい場合は往々にしてありますが、少なくとも途方もなく複雑怪奇なものではありません。
実際に、球体をレンダリングするための distance function を見てみれば、私の言いたいことが理解できると思います。実際に GLSL 内で利用できる球体の distance function は以下のようになります。
球体の distance function の例
const float sphereSize = 1.0; // 球の半径
float distanceFunc(vec3 p){
return length(p) - sphereSize;
}どうでしょう。球体を描くための distance function は、なんとたった一行で表わすことができます。
上記のコードでは float 型の定数 sphereSize に球体の半径を入れておき、GLSL のビルトイン関数である length を使って一行だけコードが走っています。この distance function が受け取る引数は vec3 型になっていますね。ここに、その時点でのレイの先端座標を渡すわけです。戻り値は float 型であり、これがレイの先端と球体との最短距離になるわけです。
distance function が非常にシンプルな作りになっているということは、上記のコードを見て十分に理解してもらえるのではないでしょうか。
球体の distance function
さて、球体の distance function が非常にシンプルに記述できるということは理解できたでしょうか。
しかし、どうして先ほどのような簡素なコードで球体をレンダリングすることができるのでしょう。これについてはクエスチョンマークが浮かんでしまう人も多いかもしれません。
球体はご存じのとおり、どの方向から眺めても見た目が変わらない物体です。このことから、球は 3D プログラミングにおけるもっとも単純で基本的なオブジェクトと言ってもいいでしょう。球は先述のとおりどの方向から見ても同じ外見です。つまりこれは言い換えれば、位置とその半径さえわかっていれば容易に扱うことができるということでもあります。
ここで、先ほどの distance function を思い出してみましょう。
球体の distance function の例
const float sphereSize = 1.0; // 球の半径
float distanceFunc(vec3 p){
return length(p) - sphereSize;
}一番最初にこの distance function が呼び出されるとき、レイはまだ一切伸ばされてはいないはずです。つまり、最初に呼び出されたときに distance function の引数に渡されるのは、カメラの置かれている座標になることがわかります。
ここで仮にカメラが (0.0, 0.0, 3.0) に置かれていると仮定して考えてみてください。GLSL のビルトイン関数である length は、ベクトルの大きさ(長さと考えるとわかりやすいかも)を float 型のデータとして返してきます。
ここではベクトルの大きさの計算方法は割愛しますが、カメラの置かれている (0.0, 0.0, 3.0) という座標を length に渡すと 3.0 を返すはずです。となると、distance function のなかでは 3.0 - sphereSize という計算が行われ、戻り値は 2.0 となります。
この結果から次のようなことがわかります。
- 球の半径は 1.0 である
- 球は原点
(0.0, 0.0, 0.0)に置かれている - カメラは
(0.0, 0.0, 3.0)に置かれている - カメラと球の表面との間の距離は 2.0 である
どうですか? 見事に、カメラの位置と球の表面との、最短距離が算出できているのがわかりますね。
今回解説している distance function は、引数としてレイのその時点での先端の座標ひとつしか受け取りません。このため、球の位置が原点に限定されてしまっています。しかし、球体の座標位置も引数として受け取るように改造すれば、球体の位置を任意にずらしてレンダリングすることも簡単にできることがわかりますね。
このように、distance function は比較的シンプルな構造で記述できるのです。もちろん、正しく最短距離を返す構造にしておかなければなりませんが、少なくとも球体の場合はたった一行で必要な処理を行うことができてしまうのです。なんだかちょっと不思議ですね。
マーチングループ
さて、distance function について理解できたら、続けて実際に GLSL のコードを見ながら概念を理解していきましょう。
前回、そして今回の冒頭でも、何度か書いたようにレイマーチングはレイを徐々に伸ばしていくことでオブジェクトを認識します。レイを、徐々に、伸ばす。このことからもわかるように、レイマーチングでは GLSL のコードの中で for 文などによるループ構造を記述してやる必要があります。
ループの中から複数回 distance function を呼び出して、最短距離を算出 ⇒ レイを伸ばす ⇒ 最短距離を算出 ⇒ レイを伸ばす……という作業を繰り返します。レイとオブジェクト間の距離が十分に小さくなった時点でオブジェクトとレイが衝突したと判断するわけです。このループ構造のことを、マーチングループと当サイトでは呼ぶこととします。
それではこれらの概念を踏まえた上で、フラグメントシェーダのコードを見てみましょう。
フラグメントシェーダのコード
precision mediump float;
uniform float time;
uniform vec2 mouse;
uniform vec2 resolution;
const float sphereSize = 1.0; // 球の半径
float distanceFunc(vec3 p){
return length(p) - sphereSize;
}
void main(void){
// fragment position
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, resolution.y);
// camera
vec3 cPos = vec3(0.0, 0.0, 2.0);
vec3 cDir = vec3(0.0, 0.0, -1.0);
vec3 cUp = vec3(0.0, 1.0, 0.0);
vec3 cSide = cross(cDir, cUp);
float targetDepth = 1.0;
// ray
vec3 ray = normalize(cSide * p.x + cUp * p.y + cDir * targetDepth);
// marching loop
float distance = 0.0; // レイとオブジェクト間の最短距離
float rLen = 0.0; // レイに継ぎ足す長さ
vec3 rPos = cPos; // レイの先端位置
for(int i = 0; i < 16; i++){
distance = distanceFunc(rPos);
rLen += distance;
rPos = cPos + ray * rLen;
}
// hit check
if(abs(distance) < 0.001){
gl_FragColor = vec4(vec3(1.0), 1.0);
}else{
gl_FragColor = vec4(vec3(0.0), 1.0);
}
}前回のサンプルでは、カメラを定義してレイを算出するところまでは解説しましたね。
今回から登場しているのは、コメントで marching loop と書かれているところから下の部分になります。
ループに入る前に、いくつかの変数を初期化しているのがわかると思います。必要となるのは、その時点での最短距離を保持するための float 型変数である distance 、そしてレイに継ぎ足す長さの合計を保持するための rLen 、そしてその時点でのレイの先端位置を保持するための vec3 型変数 rPos です。
先ほども解説したとおり、レイの原点の初期位置はカメラの位置です。ループが始まる前の時点で、まずカメラの座標が rPos に代入されているのが見てとれると思います。各種の初期化が済んだら、ループを回して最短距離を算出していきます。
マーチングループ
for(int i = 0; i < 16; i++){
distance = distanceFunc(rPos);
rLen += distance;
rPos = cPos + ray * rLen;
}マーチングループの部分だけを抜粋しました。
ループ処理を行っている部分をよく見ると、今回は 16 回のループが組まれていることがわかりますね。このループする回数は、どのくらいの広さの空間を対象とするのかや、どのようなオブジェクトをどのくらいの個数レンダリングするのかによって、ケースバイケースでいろいろと変わってきます。今回は、それほど広い空間をレンダリングする必要がないこと、また対象オブジェクトも球体が一個だけなので、実際には 16 回もループを回す必要はありません。ですから今回のサンプルにおけるループ回数には深い意味はありません。
重要なのは、ループの中身ですね。
真っ先に distance function が呼ばれているのがわかると思います。ここで返された最短距離を distance という変数に代入した後、レイを最短距離分だけ伸ばしているのも、コードをよく見るとわかると思います。
このループには、変数 distance の値に応じてループを抜けるような処理が入っていません。ですから、最低でもフラグメントシェーダが各ピクセルを処理していく際に、必ず 16 回ずつループすることになります。※マーチングループの中で距離に応じてループを抜ける処理を書いてはいけないということではありません。今回のサンプルではたまたまこのように実装しているだけです。
ループ構造を抜けた後に、変数 distance の中身を見て処理を分岐している部分があります。
最短距離に応じて色分け
// hit check
if(abs(distance) < 0.001){
gl_FragColor = vec4(vec3(1.0), 1.0);
}else{
gl_FragColor = vec4(vec3(0.0), 1.0);
}ここで、最短距離が十分に小さい値であればレイがオブジェクトと衝突していると判断して出力する色を白に、そうでない場合には黒に、といった具合に分岐しています。
ここでは distance を GLSL のビルトイン関数 abs に渡して絶対値で処理しているというのがポイントです。
というのも、オブジェクトとレイの先端位置の関係によっては、レイがオブジェクトを突き抜けてしまうケースが考えられます。実際には、レイが突き抜けてしまったとしても計算結果は破たんしません。これは、結果的にレイの向き(正負)が逆転してしまい、その上で次回の distance function が呼び出されるからです。
しかし、単純に if(distance < 0.001) というようなコードを書いてしまうと、レイがオブジェクトを突き抜けている場合にすべて無条件で衝突と判定されてしまうため、絶対値を取るような実装になっているわけですね。
まとめ
さていかがでしたか。少々駆け足でしたが、レイマーチングの基本について理解できたでしょうか。
今回解説したように、distance function とマーチングループを組み合わせることで、レイがオブジェクトと衝突しているかどうかを判断することができるようになります。そして、distance function を工夫してやることで、もちろん球体以外のオブジェクトをレンダリングすることもできるようになります。
球体の場合には、その構造がとてもシンプルなこともあり、非常に簡潔なコードで distance function を記述することができました。ほかの形状のオブジェクトを扱う場合でも、割とそのコードは簡素なものになることが多いです。もちろん、複雑なことをやろうとすればするほどコードが難しくはなります。しかし基本的な図形に関しては、そこまで大変なコードを記述しなくても実装できてしまうことが多いです。
今回のサンプルは、派手さは一切ありません。しかし、レイマーチングの基本的な実装については必要な概念がしっかり含まれています。
次回以降、今回のサンプルがベースとなって、様々に拡張していくことになるでしょう。少し難しい部分もあるかもしれませんが焦らずじっくり取り組んでみていただければと思います。
実際に動作するサンプルはいつものように以下のリンクから。
