クォータニオンと minMatrixb.js
今回のサンプルの実行結果
クォータニオンを扱うライブラリ
前回はクォータニオンとはなんなのか、またその計算方法とはどのようなものなのか、などを中心に解説しました。しかし、前回の内容だけでは、実際にクォータニオンを使ったわけではないのでいまひとつ理解が深まりきっていない部分があると思います。
今回のテキストでは、実際にクォータニオンを利用したプログラムを組んでみます。そのなかで、三次元空間上の座標をクォータニオンによって変換し、回転させます。
正直に書いてしまうと、今回の解説に用いるサンプルの内容は、別にクォータニオンを使わなくても比較的簡単に実現できてしまうような簡易なものです。しかし、クォータニオンを使うことによって、それが直感的に実装できることは実感できると思います。
クォータニオン周辺の処理は、当サイトのオリジナルライブラリである minMatrixb.js を使って実装します。このライブラリには、基本的な行列演算を実装した姉妹ライブラリである minMatrix.js に含まれる処理はもちろんのこと、クォータニオンを扱うための実装が新たに含まれています。
クォータニオンに関する処理は、恐らく、非常に難しいイメージがあると思います。ですがこの minMatrixb.js を利用すれば比較的簡単にクォータニオンを扱うことができるはずです。
minMatrixb.js の詳細なリファレンスは別テキストとして用意してありますのでそちらを参照していただくとして、今回のテキストでは使い方をメインに解説します。
クォータニオンでカメラ制御
今回のサンプルでは、クォータニオンを使ったカメラ制御を行なってみます。
まずはカメラ制御のおさらいから。
当サイトのあらゆるサンプルでは、カメラはビュー座標変換行列によって定義していましたよね。ビュー座標変換行列を生成するにあたり、minMatrix.js に実装されている matIV.lookAt メソッドを使っていました。
ここで登場する lookAt メソッドでは、カメラの座標、カメラの注視点、カメラの上方向を引数として与える必要がありましたね。クォータニオンを使ってカメラを制御するということは、これらのカメラに関する情報をクォータニオンを用いて操作しなければなりません。
今回作成するサンプルでは、三次元空間上の原点にトーラスをレンダリングします。そして、そのトーラスの周辺を、円を描くように動きながら撮影するカメラを実装してみます。具体的には、原点から見て手前の位置(Z 値がプラスの位置)に置いたカメラを X 方向を軸に原点を中心として回転させながら、尚且つ、常に原点を見つめるようにして動かすことが目的となります。
言葉ではちょっとイメージし難いかもしれませんが、次の図に示すようなイメージです。
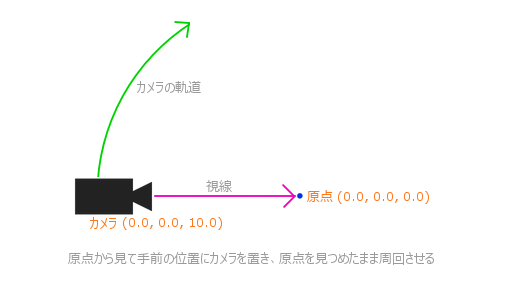
さて、カメラにこのような挙動をさせるためには、どのようなプログラムを組めばいいでしょうか。
ここでポイントとなるのは、ビュー座標変換行列を生成する際に必要となる、カメラに関する情報(パラメータ)の意味をよく考えることです。
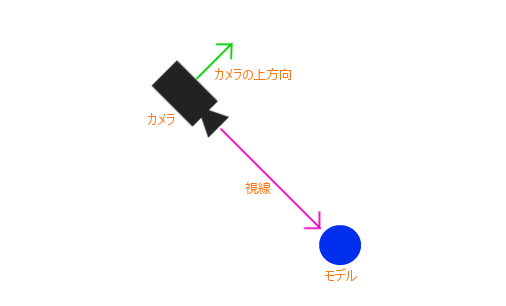
まず、回転を行なっていない状態でのカメラは次のような感じでモデル(原点)を見つめています。
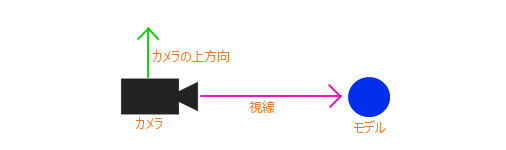
モデルは原点にレンダリングされるようにするので、その位置を純粋に見つめるカメラがある状態ですね。
この状態から、カメラを動かしていくわけですが、カメラは常にモデルを見つめるようにしなければなりません。このとき、カメラの座標だけを回転させると以下の図のような状況になります。
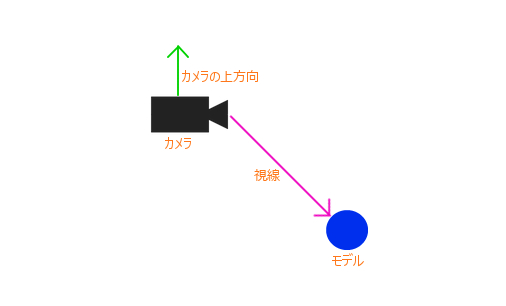
これは明らかにおかしいですね。
カメラの座標が移動したとしても、カメラの上方向もそれと連動して変化するようにしなければ、正しいレンダリング結果を得ることはできないわけです。
たとえばフライトシミュレータのようなプログラムで飛行体をレンダリングするようなシーンがあったとして、その飛行体の周囲をカメラが回転しながら撮影するような状況を考えると、このカメラの上方向というパラメータが結構ネックになってきたりするわけです。
正しくカメラの座標とカメラの上方向を変換し、本来意図している結果を得られた場合には、カメラの挙動は以下のような状態になるはずですね。
今回のサンプルで目指すのは、上記の図のようなカメラ制御です。これを、クォータニオンを使って実装します。
クォータニオンによるベクトルの回転
前回のテキストで解説したように、クォータニオンでベクトルを回転させる際には、回転要素を持つクォータニオンと、その共役四元数を使って計算を行ないます。
当サイトオリジナルのライブラリである minMatrixb.js には、このような三次元ベクトルを回転させる処理を補助するメソッドが実装されています。それが qtnIV.toVecIII メソッドです。
このメソッドの内部では、引数として与えられたクォータニオンの共役四元数を自動生成して計算を行ないます。回転要素を持つクォータニオン、回転させたいベクトル、計算結果が格納されるベクトルの三つの引数を与えてメソッドを呼び出すだけで、簡単にベクトルを回転させることが可能です。
※以下、q は qtnIV オブジェクトのインスタンスです
toVecIII メソッドの記述例
q.toVecIII([0.0, 0.0, 10.0], quaternion, vector);当然と言えば当然ですが、この toVecIII メソッドに渡すクォータニオンには、あらかじめ回転を与えておく必要があります。前回のテキストで、クォータニオンに回転を与える方法についても解説しましたが、minMatrixb.js を使えば簡単にクォータニオンに回転成分を与えることが可能です。
クォータニオンに回転を与えるには qtnIV.rotate メソッドを使います。このメソッドには、回転角度、軸ベクトル、結果を格納するクォータニオンの三つを引数として渡します。
rotate メソッドの記述例
q.rotate(radian, [1, 0, 0], quaternion)上記のように記述すれば、X 軸を中心として radian 分だけ回転するクォータニオンが生成できます。このようにして生成したクォータニオンを使って toVecIII メソッドを実行すれば、簡単に三次元ベクトルを回転させることが可能なわけですね。
先にも書いたとおり、今回はカメラを制御するためにクォータニオンを使います。具体的には、カメラの座標とカメラの上方向の二つに対してクォータニオンを適用することで、原点に置かれたモデルの周囲を回転しながら、原点を見つめ続けるカメラを実装できます。
サンプルのコード
今回のサンプルは、以前のテキストで取り扱った点光源によるライティングを行ないつつ、カメラの制御をクォータニオンで行ないます。点光源を実装した際のシェーダをそのまま使っているので、HTML に関する解説は割愛します。
javascript プログラムの中では、クォータニオンの初期化と、カメラに関するパラメータの宣言を行なっておきます。
あとは、ループ処理のなかでリアルタイムにクォータニオンに与える回転要素を変化させながらレンダリングすればいいですね。
クォータニオンの初期化処理
// 四元数の生成と初期化
var q = new qtnIV();
var xQuaternion = q.identity(q.create());上記のような処理が走ると、変数 xQuaternion には単位化されたクォータニオンが入ります。
続いて、このクォータニオンに回転を与え、そこからさらにベクトルにクォータニオンを適用します。
クォータニオンの回転とベクトルへの適用
// カメラの座標
var camPosition = [0.0, 0.0, 10.0];
// カメラの上方向を表すベクトル
var camUpDirection = [0.0, 1.0, 0.0];
// カウンタの宣言
var count = 0;
// 恒常ループ
(function(){
// canvasを初期化
gl.clearColor(0.0, 0.0, 0.0, 1.0);
gl.clearDepth(1.0);
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
// カウンタをインクリメントする
count++;
// カウンタを元にラジアンを算出
var rad = (count % 180) * Math.PI / 90;
var rad2 = (count % 720) * Math.PI / 360;
// クォータニオンによる回転
q.rotate(rad2, [1, 0, 0], xQuaternion);
q.toVecIII([0.0, 0.0, 10.0], xQuaternion, camPosition); // *1
q.toVecIII([0.0, 1.0, 0.0], xQuaternion, camUpDirection); // *2
// ビュー×プロジェクション座標変換行列
m.lookAt(camPosition, [0, 0, 0], camUpDirection, vMatrix);
m.perspective(45, c.width / c.height, 0.1, 100, pMatrix);
m.multiply(pMatrix, vMatrix, tmpMatrix);
// 中略
// ループのために再帰呼び出し
setTimeout(arguments.callee, 1000 / 30);
})();途中の処理はだいぶ省略してしまっていますが、ループのなかでやっていることの要点は上記のコードを見ればわかると思います。
カメラの座標を格納するための変数 camPosition の宣言と、カメラの上方向を格納するための変数 camUpDirection の宣言がされていますね。ループの中では、毎回カウンタをインクリメントしながら、カウンタの値を使ってラジアンを算出しています。ここで算出されたラジアンを使って、まずはクォータニオンを回転させているのがわかると思います。
クォータニオンに回転を与えることさえできれば、あとはそれを使ってベクトルを回転させるだけです。上記のコードのなかで *1 というコメントが付いている行がカメラの座標を変換している部分、そして *2 の行がカメラの上方向を示すベクトルを回転させている部分ですね。
uniform 変数の登録や描画命令の発行は省略していますが、メインループのなかでクォータニオンをどのように扱うのかはわかっていただけるかと思います。
まとめ
今回のサンプルを実行すると、トーラスの周囲を、トーラスを見つめながら周回するカメラの挙動を確認できると思います。正直なところ、今回のような簡単な回転を扱うだけなら、わざわざクォータニオンを使うまでもないのかもしれません。しかし、シンプルな設計のサンプルを用いたほうが、より理解が深まるのではと思いこのような実装にしました。
minMatrixb.js と、それによって実装できるクォータニオンを使ってみれば、ベクトルを回転させる処理が非常に簡単に記述できることがわかると思います。minMatrixb.js のソースを見てみれば、クォータニオンを操作するための計算方法についてもぐっと理解が深まるでしょう。
今回はまだ、クォータニオンを使った基本的なことしかやっていません。何事もまずは基本的なことをしっかりと理解したほうが、あとあと何かと役に立ちます。
サンプルへのリンクはいつものように下のほうにあります。若干地味なサンプルですが、実際に動作するところを確認してみてください。
次回は、もっと具体的なクォータニオンの活用方法として、マウスによるモデルの回転制御をやってみます。これが実装できると、あらゆる方向から自由自在にモデルを眺めることが可能になります。
