gaussian フィルタ

今回のサンプルの実行結果
ガウシアンブラー
前回はエッジ検出の手法の一つ、laplacian フィルタを解説しました。前々回に紹介した sobel フィルタと比較すると、細い線による繊細なエッジ検出ができるのでしたね。
さて、今回はフィルタ系の処理をもう一つ取り上げます。今回のフィルタはかなり実用性の高いものです。今後様々なエフェクト処理を行なっていく上で欠かせないぼかし系処理の代表格、gaussian フィルタ(ガウシアンフィルタ)です。
ガウシアンぼかし、あるいはガウスぼかしなどと呼ばれるぼかし処理は、様々なペイントソフトやフォトレタッチソフトにも搭載されています。そもそも[ ぼかす ]という処理に優劣があるのかというところに疑問を抱く方ももしかしたらいるかもしれませんが、gaussian フィルタが優れているポイントはいくつかあります。
- 処理結果が自然で美しく仕上がる
- 大きくぼかしを掛けることが可能
- その割に高速で処理できる
3D プログラミングでは、いまやぼかし系処理はある意味必須のテクニックです。一度、バックバッファに描き込んだレンダリング結果をぼかしてから合成しグレアを表現したり、背景となる遠方の風景だけをぼかして処理したり、ぼかし処理が活躍する場面は非常に多いです。
今回のテキストを通して、ぼかし処理の王道ガウシアンぼかしを是非習得してください。
gaussian フィルタの特徴
以前、フレームバッファを活用してレンダリング結果をぼかすという処理を解説したことがありました。
このときは一度フレームバッファに描き込んだフラグメントのうち、5 x 5 の範囲を対象として加重平均を取りました。これから描き込もうとしているフラグメントの周囲の色を加味することで、全体的にぼやけた印象のレンダリング結果を生成することができるのでしたね。
このときは、純粋に 5 x 5 の領域を全てサンプリングしたので、一つのフラグメントを描き込むために 25 ピクセルもの領域を参照する必要がありました。
たった一つのフラグメントの色を決定するために、25 パスもの処理がフラグメントシェーダ内で走ることになるわけですから、これはけして軽い処理ではないことが容易に想像できますね。そう、ぼかし処理は美しいエフェクトを実装するために必要不可欠な処理でありながら、実際には気軽に使えるような軽い処理ではないのです。
さて、ここで gaussian フィルタの出番です。
先にも書いたように、gaussian ブラーは比較的高速に動作します。しかも、高速な割に大きくぼかすことができるという、まさに良いとこ取りな特徴があります。なぜこのようなことが可能なのでしょうか。
実はこれには、gaussian フィルタに使われるガウス関数が関係しています。
ガウスの由来は人名です。ドイツの物理学者であり、数学者ですね。
ガウスさんの考案したガウス関数を用いると、計算結果は以下のように釣り鐘型になります。
ガウス関数の結果
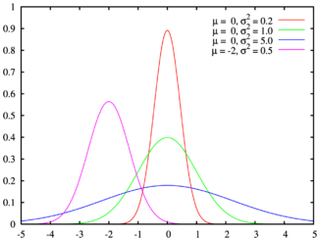
※画像は wikipedia より引用
このガウス関数によって導き出された釣り鐘の頂点部分をこれから処理しようとしているフラグメントの係数として使います。周囲のピクセルには、同じようにガウス関数を使って導き出された係数を適用して処理します。
処理しようとしているフラグメントから遠い位置にあるピクセルほど係数が小さくなるのは先ほどのグラフを見ればわかりますね。そして、先ほどのグラフをよく見ると、縦長の釣り鐘型もあるし、横長の偏平な釣り鐘型もありますね。これはガウス関数に渡すパラメータ一つで簡単に調整できます。
つまり、ガウス関数を用いると、小さくぼかすための係数も、大きくぼかすための係数も、パラメータ一つで簡単に算出することが可能になります。また、先ほどのグラフは二次元のグラフでしたが、ガウス関数は三次元で計算した場合でも、釣り鐘の頂点部分からどの程度の距離にあるのかによって、円形に正しく係数を算出することができます。
さらに、ガウス関数を三次元で用いる場合には x 方向と y 方向を切り離して処理することができます。実はこれが非常に重要です。
たとえば、以前のテキストで解説したときに用いた 5 x 5 のカーネルでは、一つのフラグメントを処理するために 25 パス必要でしたよね。
これは単純に 5 x 5 = 25 という処理回数が必要になるからです。しかし、ガウス関数を用いると x と y を切り離して別々に処理することができるため、5 + 5 = 10 という具合に、パスを大幅に削減できます。これが、gaussian フィルタが高速に動作するということの答えです。
ぼかす範囲が大きくなればなるほど、この恩恵は大きくなります。10 x 10 の範囲を参照するぼかし処理を実装しようと思ったら、普通にぼかし処理を行なうには一つのフラグメントあたり 100 パスもの処理が必要になりますが、gaussian フィルタならたったの 20 パスで済みます。これはとてつもなく大きな処理軽減に繋がりますね。
シェーダの実装
さて、ガウス関数を用いてブラー処理を行なう gaussian フィルタ。そのシェーダを見てみます。
今回はフラグメントシェーダ内でブラー処理を行いますが、ガウス関数によって算出された各フラグメントに掛け合わせる係数は uniform 変数としてメインプログラムから受け取るようにします。
また、今回のサンプルでは、これから処理しようとしているフラグメントを中心として、上下左右にそれぞれ 9 ピクセルの範囲をブラー処理の範囲としてサンプリングします。中心 1 ピクセル、上下左右にそれぞれ 9 ピクセルですから、要するに 19 x 19 の範囲をサンプリングすることになります。これを gaussian フィルタではなく真面目に全てサンプリングすると実に 361 パスも必要になります。やってみるまでもなく、恐ろしく重い処理になりますね。
今回は gaussian フィルタを用いることで、これが 38 パスで実現できます。しかも、ぼかし具合は先ほども書いたようにパラメータ一つで簡単に調整できますので、非常に実用的です。
それではシェーダのソースを見てみましょう。まずは無駄に長いフラグメントシェーダのソースから。
gaussian フィルタ用フラグメントシェーダ
precision mediump float;
uniform sampler2D texture;
uniform bool gaussian;
uniform float weight[10];
uniform bool horizontal;
varying vec2 vTexCoord;
void main(void){
float tFrag = 1.0 / 512.0;
vec2 fc;
vec3 destColor = vec3(0.0);
if(gaussian){
if(horizontal){
fc = vec2(gl_FragCoord.s, 512.0 - gl_FragCoord.t);
destColor += texture2D(texture, (fc + vec2(-9.0, 0.0)) * tFrag).rgb * weight[9];
destColor += texture2D(texture, (fc + vec2(-8.0, 0.0)) * tFrag).rgb * weight[8];
destColor += texture2D(texture, (fc + vec2(-7.0, 0.0)) * tFrag).rgb * weight[7];
destColor += texture2D(texture, (fc + vec2(-6.0, 0.0)) * tFrag).rgb * weight[6];
destColor += texture2D(texture, (fc + vec2(-5.0, 0.0)) * tFrag).rgb * weight[5];
destColor += texture2D(texture, (fc + vec2(-4.0, 0.0)) * tFrag).rgb * weight[4];
destColor += texture2D(texture, (fc + vec2(-3.0, 0.0)) * tFrag).rgb * weight[3];
destColor += texture2D(texture, (fc + vec2(-2.0, 0.0)) * tFrag).rgb * weight[2];
destColor += texture2D(texture, (fc + vec2(-1.0, 0.0)) * tFrag).rgb * weight[1];
destColor += texture2D(texture, (fc + vec2( 0.0, 0.0)) * tFrag).rgb * weight[0];
destColor += texture2D(texture, (fc + vec2( 1.0, 0.0)) * tFrag).rgb * weight[1];
destColor += texture2D(texture, (fc + vec2( 2.0, 0.0)) * tFrag).rgb * weight[2];
destColor += texture2D(texture, (fc + vec2( 3.0, 0.0)) * tFrag).rgb * weight[3];
destColor += texture2D(texture, (fc + vec2( 4.0, 0.0)) * tFrag).rgb * weight[4];
destColor += texture2D(texture, (fc + vec2( 5.0, 0.0)) * tFrag).rgb * weight[5];
destColor += texture2D(texture, (fc + vec2( 6.0, 0.0)) * tFrag).rgb * weight[6];
destColor += texture2D(texture, (fc + vec2( 7.0, 0.0)) * tFrag).rgb * weight[7];
destColor += texture2D(texture, (fc + vec2( 8.0, 0.0)) * tFrag).rgb * weight[8];
destColor += texture2D(texture, (fc + vec2( 9.0, 0.0)) * tFrag).rgb * weight[9];
}else{
fc = gl_FragCoord.st;
destColor += texture2D(texture, (fc + vec2(0.0, -9.0)) * tFrag).rgb * weight[9];
destColor += texture2D(texture, (fc + vec2(0.0, -8.0)) * tFrag).rgb * weight[8];
destColor += texture2D(texture, (fc + vec2(0.0, -7.0)) * tFrag).rgb * weight[7];
destColor += texture2D(texture, (fc + vec2(0.0, -6.0)) * tFrag).rgb * weight[6];
destColor += texture2D(texture, (fc + vec2(0.0, -5.0)) * tFrag).rgb * weight[5];
destColor += texture2D(texture, (fc + vec2(0.0, -4.0)) * tFrag).rgb * weight[4];
destColor += texture2D(texture, (fc + vec2(0.0, -3.0)) * tFrag).rgb * weight[3];
destColor += texture2D(texture, (fc + vec2(0.0, -2.0)) * tFrag).rgb * weight[2];
destColor += texture2D(texture, (fc + vec2(0.0, -1.0)) * tFrag).rgb * weight[1];
destColor += texture2D(texture, (fc + vec2(0.0, 0.0)) * tFrag).rgb * weight[0];
destColor += texture2D(texture, (fc + vec2(0.0, 1.0)) * tFrag).rgb * weight[1];
destColor += texture2D(texture, (fc + vec2(0.0, 2.0)) * tFrag).rgb * weight[2];
destColor += texture2D(texture, (fc + vec2(0.0, 3.0)) * tFrag).rgb * weight[3];
destColor += texture2D(texture, (fc + vec2(0.0, 4.0)) * tFrag).rgb * weight[4];
destColor += texture2D(texture, (fc + vec2(0.0, 5.0)) * tFrag).rgb * weight[5];
destColor += texture2D(texture, (fc + vec2(0.0, 6.0)) * tFrag).rgb * weight[6];
destColor += texture2D(texture, (fc + vec2(0.0, 7.0)) * tFrag).rgb * weight[7];
destColor += texture2D(texture, (fc + vec2(0.0, 8.0)) * tFrag).rgb * weight[8];
destColor += texture2D(texture, (fc + vec2(0.0, 9.0)) * tFrag).rgb * weight[9];
}
}else{
destColor = texture2D(texture, vTexCoord).rgb;
}
gl_FragColor = vec4(destColor, 1.0);
}自分で言うのもなんですが、酷いソースですなぁ。
今回のフラグメントシェーダでは、そもそもフィルタを掛けるかどうか、そして掛けるとしたら縦方向なのか横方向なのか、これらはメインプログラムから送られてきた uniform 変数によって判断し分岐します。
先ほども書いたように、gaussian フィルタでは縦と横の処理を切り離して行うことができます。要は、まず始めに横なり縦なり、どちらかの方向にぼかした状態のレンダリング結果をフレームバッファに描きこみます。
横方向へのぼかし
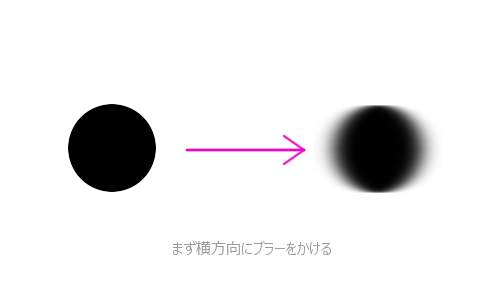
続いて、一方向ぼかしのフレームバッファをテクスチャとして読み込んでから、もう一方の方向に対するぼかしを掛けます。
縦方向のぼかし
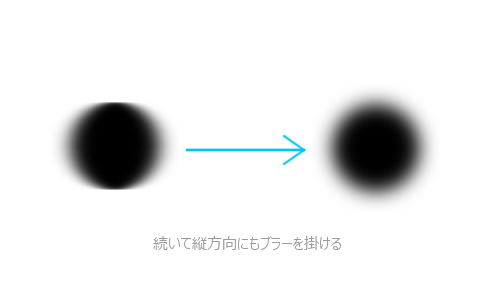
この二段構えを行なうために、フラグメントシェーダ内で真偽値を使って処理を分岐できるようにしているわけですね。
さて、一方でこのフラグメントシェーダと対になる頂点シェーダはどうでしょうか。さらっとソースを見てみます。
頂点シェーダのソース
attribute vec3 position;
attribute vec2 texCoord;
uniform mat4 mvpMatrix;
varying vec2 vTexCoord;
void main(void){
vTexCoord = texCoord;
gl_Position = mvpMatrix * vec4(position, 1.0);
}はい、滅茶苦茶簡素ですね。フラグメントシェーダがだいぶ壮大だった分、余計に簡素に見えます。頂点シェーダでは特別なことは何もしません。この頂点シェーダには正射影での座標変換行列が入ってくるようにしましょう。グレイスケールや各種フィルタ処理で行なったのと同様、正射影で板ポリゴンを一枚表示するためだけの頂点シェーダです。
その他の実装も見てみる
さて、先ほども少し触れましたが、今回はフレームバッファをうまく活用しないといけません。
手順としては以下のようにしてやる必要があります。
- フレームバッファを二つ用意する
- 一つ目のフレームバッファにシーンをレンダリング
- 二つ目のフレームバッファに横ぼかしでレンダリング
- canvas に縦ぼかしで最終的なレンダリング
一度横方向にぼかしてから、それをテクスチャとして読み込み、今度は縦ぼかしでレンダリングを行ないます。この実装のせいで、どうしてもフレームバッファが二つ必要になりますので注意しましょう。
まず最初に一つ目のフレームバッファに、普通にライティングを行ないながらトーラスをレンダリングします。この一つ目のフレームバッファをテクスチャとして設定したら、続いて二つ目のフレームバッファに、横方向で gaussian フィルタを適用してレンダリングを行ないます。
この時点では、まだ横方向のブラーが掛かっただけの状態ですので、今度は二つ目のフレームバッファをテクスチャとして設定して、縦方向のブラーを掛けながら canvas に最終的なシーンをレンダリングして完成となります。
また、ガウス関数の係数を求める処理も必要になりますので、その部分だけを抜粋したコードを見てみましょう。
ガウス関数から係数を算出する
// gaussianフィルタの重み係数を算出
var weight = new Array(10);
var t = 0.0;
var d = eRange.value * eRange.value / 100;
for(i = 0; i < weight.length; i++){
var r = 1.0 + 2.0 * i;
var w = Math.exp(-0.5 * (r * r) / d);
weight[i] = w;
if(i > 0){w *= 2.0;}
t += w;
}
for(i = 0; i < weight.length; i++){
weight[i] /= t;
}ここで登場している eRange は、HTML 内に埋め込まれた input 要素( Range タイプ)です。
input 要素の値を使って、ガウス関数に与えるパラメータを変化させるためにこのような仕様になっています。
ガウス関数を実際に使っているのは Math.exp を使っている部分。算出された重み係数は、いったん変数 w に入ります。その後、変数 t に変数 w の値をどんどん加算していきます。この変数 t は最終的に重み係数を正規化するために使います。
この一連の処理によって生成された配列 weight をシェーダに送ってやることで、シェーダ内で gaussian フィルタを掛けることができるわけですね。
ちなみに、変数 d に入る数値が大きくなればなるほど、ガウス関数によって生成される値は偏平型の釣り鐘になっていきます。つまり、変数 d とブラーのかかる強さは比例します。変数 d が大きくなればなるほど大きなぼかし処理が掛かるというわけです。
まとめ
さて gaussian フィルタ、いかがでしたでしょうか。
冒頭でも書いたとおり、ブラー系の処理はエフェクト関連の処理には欠かせない存在です。できる限り低コストで、美しいブラー処理を行ないたいと考えた場合には gaussian フィルタは有用な選択の一つだと言っていいと思います。
実装としてはフレームバッファを二つ使ったり、ガウス関数を用いたりと、若干わかりにくい部分もあったかと思います。また、ガウス関数をちゃんと理解しようと思ったら、数学的な知識も必要になるのでさらに大変です。
数学的なことはイマイチわからなくても、とりあえずこのサンプルを読み解けば利用することはできるはずです。今後はブラー処理を伴うエフェクトのサンプルも登場してくるかもしれません。ここでしっかりと習得しておいて損はないので、がんばってください。
いつものように、実際に動作するサンプルへのリンクが以下にあります。実物を操作しながら、どのような効果が得られるのか観察してみてください。
