3D 描画の基礎知識
二次元と三次元
三次元空間――それは、我々の生きているこの現実世界に他なりません。
三次元の世界では、全てのものに縦と横、そして奥行きが存在します。そしてそれを再現しようとするのが、リアルタイム 3D レンダリングですね。しかし、三次元空間を再現しようとするとき、それを出力する先は普通、二次元のモニター上です。
パソコンや、モバイル機器などのあらゆるデバイスは、二次元のモニター上に情報を出力します。少なくとも現代ではいまのところ、奥行きのある空間を物理的に実現するデバイスはありませんね。まぁ、研究所の分厚い扉の向こう側にはあるのかもしれませんが、一般家庭には普通そんなものはありません。
WebGL を使って擬似的に三次元空間をシミュレートしたとしても、最終的にはそれをモニターという二次元空間に出力しなくてはなりません。奥行きによる前後関係や、遠近法による伸縮拡大を加味して、どこになにがどんなふうに描かれるのか、算出しなければならないわけです。
OpenGL にしても、DirectX にしても、この三次元から二次元への変換を行なう基本的な計算手法はほとんど変わりません。同様の理由で、WebGL でも基本は一緒です。当たり前と言えば当たり前ですが。
右手? 左手? 座標系の話
3D の計算の基本は同じとは言っても、DirectX と OpenGL の間にはちょっとした違いがあったりします。
DirectX と OpenGL の違いとしてよく挙げられるのが座標系の違いです。よく、左手系とか右手系とか、そんなふうに言われたりします。ちなみに、OpenGL はいわゆる右手座標系です。
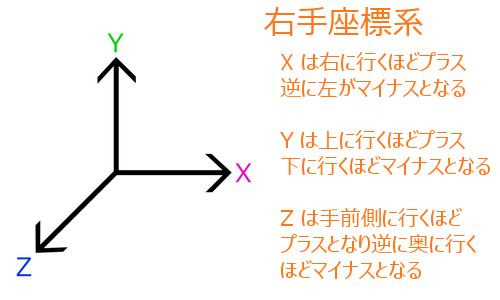
これに対して DirectX は左手座標系になります。
図で表すと次のような感じですね。
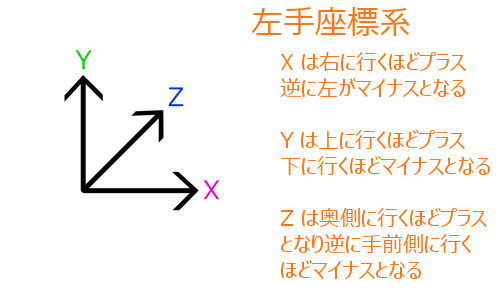
これをよくよく比較してみると、要するに Z 座標の扱いが異なっている(反転している)だけなのだということがわかります。X 座標と Y 座標に関しては、どちらの座標系を用いた場合でも扱いは同じです。
Z 座標の扱いが異なるという点を除けば、どちらの座標系なのかはあまり深い意味はありませんので、難しく考える必要はないでしょう。WebGL は OpenGL の流れを汲むので、当然右手座標系ですので注意しましょう。
座標変換について知る
Z 座標の扱いの違いはあるものの、DirectX であれ OpenGL であれ、シミュレートした三次元の情報を最終的には二次元に変換しなければなりません。始めにも書いたように、最終的に画像が映し出されるモニターは常に二次元だからですね。
その際に必要となるのが座標変換と呼ばれる一連の計算です。座標の変換には、大きく分けて三つの種類があり、これらを正しく組み合わせることで、最終的にモニター上のどの位置にどんなものを描き出すのかが決まります。
身近なものでたとえると、三次元の情報を二次元に変換するものの代表例としてカメラがあります。写真であれ映像であれ、カメラを通すとそれは全て二次元の情報に変換され、最終的には写真や動画として平面上で表現できる形になりますね。
頭のなかでカメラを使っているときをイメージしながら、座標変換について考えてみましょう。
モデル変換
三つある座標変換の一つ目は、モデル変換です。OpenGL の処理系ではこのモデル変換という名称が一般的ですが、DirectX 系ではワールド変換と呼ばれているものですね。
モデル変換とは、被写体となる物体が三次元空間のどの位置にあるのかを定義するための座標変換です。現実の世界とは異なり、プログラムのなかの三次元空間には世界の中心の基準となる原点という位置が定義されています。その原点から見て、被写体となるモデルが相対的にどの位置に存在しているのかを知るためにモデル変換が必要になります。
仮に、シミュレートする三次元空間にリンゴがひとつ存在しているとしたら、そのリンゴの存在する位置を定義するためにモデル変換が必要になるわけですね。
ビュー変換
三つある座標変換の二つ目はビュー変換と呼ばれます。
ビュー変換では、実際にカメラがどの位置にあるのか、そしてカメラはどこを向いているのかなどを定義します。先ほどのリンゴの話に合わせると、仮に三次元空間にリンゴが存在していたとしてもカメラがそのリンゴに向けられていなければ、リンゴが映し出されることはありませんね。他にも、たとえばカメラとリンゴとの距離が著しく離れていれば、仮にリンゴにカメラが向けられていたとしても映らないかもしれません。
カメラの位置や、その向けられている方角を決めるために行なう座標変換、それがビュー変換というわけです。
プロジェクション変換
三つある座標変換の最後の一つ、それがプロジェクション変換です。
この変換では、三次元空間のどの領域を撮影するのかなどを定義します。たとえば、横に幅広くパノラマとして撮影するのか、あるいは縦長の映像として撮影するのか、どのくらい遠くまでを撮影するのかなどを定義することができます。
一般的なカメラの場合は、レンズの前にあるもの全てを撮影しますし、どのくらい遠くまで撮影するのかなんて意識することはありませんね。しかし、プログラムが無限に広い空間をシミュレートするのは不可能です。そこで、一番手前はここから、一番遠くはここまで、というシミュレートする領域を決めて処理するわけですね。
プロジェクション変換を行なうことによって、いわゆる遠近法の効果が得られます。近くにあるものは大きく、遠くにあるものは小さく描画されるようになるわけです。
まとめ
随分長いテキストになりましたが、ざっくりと内容をまとめましょう。
プログラムが三次元空間をシミュレートするとき、最終的にはその情報を二次元のデータに変換しなければなりません。そして、三次元の座標を扱う場合には、利用するプラットフォームによって若干 Z 座標の扱いが違っているのでしたね。WebGL は OpenGL の処理系ですので、右手座標系として座標を処理します。
シミュレートした三次元空間の情報を二次元の情報に変換するために、三つの座標変換が必要になるのでしたね。それらはそれぞれ、モデル変換、ビュー変換、プロジェクション変換と呼ばれており、それらが組み合わさって最終的にディスプレイ上に何が描画されるのかが決まります。
WebGL でプログラムを組んでいく上では、今回取り上げた座標系の知識と、座標変換の知識が不可欠です。細かい部分はさておき、だいたいの意味は理解していないと今後実際に処理を記述していく際に困惑してしまうでしょう。最低限、三つの座標変換の言葉の意味くらいは覚えておきましょう。
さて、次回は WebGL を使うために準備するものについて見ていきます。お楽しみに。
