後光 表面下散乱

今回のサンプルの実行結果
光を透過する物体
前回のテキストでは、ライトの位置と視線を考慮してモデルの輪郭部分に照明効果を生み出すリムライティングを取り上げました。使われる場面はそれなりに限定されると思いますが、暗闇で強めのライトが当たっている状態や、屋外シーンでも強烈な陽の光が当たっているシーンなど、活用できる場面はいくつか考えられます。実装もそれほど難しくないので、ケースバイケースで使ってみてはいかがでしょうか。
さて、今回はリムライティングの際に登場した概念をうまく生かして、表面下散乱(subsurface scattering)をやってみたいと思います。
表面下散乱は、半透明な物体の内部(表面下)で、光が乱反射(散乱)する様子を再現するものです。人間の肌や大理石のように、完全な不透明ではなく微妙に光を透過する物体に用いられます。近年のリアルな 3DCG では、人肌をより本物らしく見せるために、様々な手法でこの表面下散乱が実装されています。
表面下散乱には先ほども書いたように様々な手法や表現があり、表面下散乱=こうすればいい、といったような画一的な正解はありません。今回実装する表面下散乱もいくつかある手法の中のひとつであり、特にモデルの後方から光が当たっている場面においてちからを発揮します。
手のひらを太陽に
幼少の頃、手のひらを太陽にかざして見てみたことがある人は多いと思います。自分などは、普段は肌色をしている手のひらが、太陽にかざすと真っ赤に見えることが不思議でなりませんでした。今となっては不思議でもなんでもないんですけどもね。
今回実装する表面下散乱は、太陽にかざした手のひらのように、モデルの向こう側からやってくる光を透過する状態を再現することが目的になります。
とは言っても、今回のサンプルではモデルの厚みだけを考慮して光の透過を計算します。本来であれば、手のひらを太陽にかざしてみると表皮の下にある骨や血管が透けて見えるはずですが、そこまでの厳密な計算はしません。カメラ側から見えるモデルの面と、モデルの裏側から撮影したカメラで見える面、この二つの面同士の距離を計測することでモデルがどの程度の厚みなのかを割り出します。
割り出された厚みが小さければ小さいほど、その物体は薄く光を透過しやすいと考えます。逆に、算出した厚みが大きい場合にはそれほど光を透過しないようにしてやります。
厚みを割り出すために
それでは、具体的にモデルの厚みを割る出すためにはどうしたらいいのか考えてみましょう。
まず真っ先に思いつくのは、カリング面を反転することで、表面と裏面とをそれぞれレンダリングしてやり厚みを計算する方法です。
図式化すると以下のようになりますね。
カリングを使ってモデルの厚みを算出する
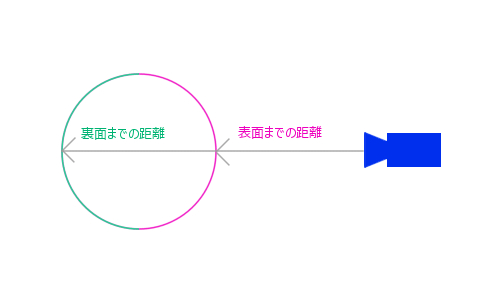
カリングをうまく使って、まずはじめに裏か表か一方の面をフレームバッファに描き込んでおき、カリング面を反転した後、もう一度モデルをレンダリングすれば深度値を比較することで厚みが計算できます。
しかし、この方法には問題があります。例えば、トーラスのようにひとつのモデルで重なり合う部分があったり、あるいは同時に複数のモデルが重なり合ったりする場合にはうまくいかない場面が出てきます。
これも、図式化してみるとよくわかるでしょう。先ほどと同じように、カリングによってレンダリングされる表面と裏面とを色分けして図式化してあります。
複数のモデルが重なり合う場面
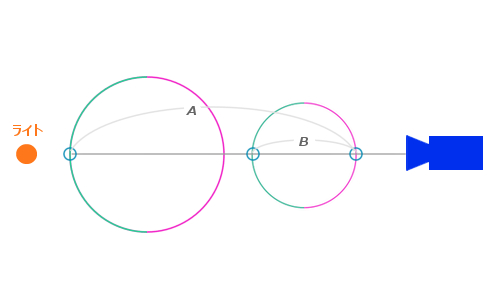
上記の図のようなシーンでは、カメラに近いほうにあるモデルは、その後ろにあるモデルの影響でほとんど光が当たらないはずです。カメラに一番近い面からライトに一番近い面までは A の距離があるはずですね。にもかかわらず、カリングの反転によって深度値を計算すると手前の面の深度は B として算出されてしまいます。この状態で単純に厚みが薄い部分ほど光を透過するようにしてしまうと、実際にはまったく光が当たっていない部分が明るく照らされてしまうような、誤った照明効果が起こってしまいます。
この問題に対処するためには、単純にカリングの反転によって深度値を判断するのではなく、純粋にモデルの裏側にカメラを持っていき、モデルの裏面をレンダリングしてやればいいですね。
モデルの向こう側から撮影したシーンの深度値と、手前側から撮影したシーンの深度値を比較してやるようにすれば、たとえ複数のモデルが重なり合っていても正しく手前面と奥面との距離を計測できます。
さらに、前回のリムライティングで行ったのと同じように、カメラとライトがどの程度向き合っているのかを加味しながら光の透過を再現してやれば、それらしい光の透過を再現できます。
重なり合ったモデルも考慮した光の透過
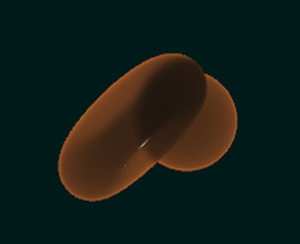
トーラスの光の透過に、後ろ側にある球体の影響が出ているのがわかりますね。
プログラムの概要
今回のプログラムは、かなり冗長な手順を踏むかたちになります。
そのことを踏まえ、まずは必要な概念をあらかじめ整理しておきます。
- モデルの裏側にカメラを置き裏面深度をバッファに描き込む
- 表側にカメラを置き裏面との深度の差分をバッファに描き込む
- 深度の差分を描き込んだバッファをブラー処理してぼかす
- 最終シーンでブラー処理した深度値を読み出しつつライティング
ポイントは、深度の差分をぼかしておくということです。
これには以前のテキストで解説したガウシアンブラーを使います。ぼかす理由としては、表面下散乱の言葉のとおり、光が拡散する様子をできるだけリアルに再現するためです。
これらの手順を踏んで動作する本テキストのサンプルは、以下のような画面になります。
サンプルの画面
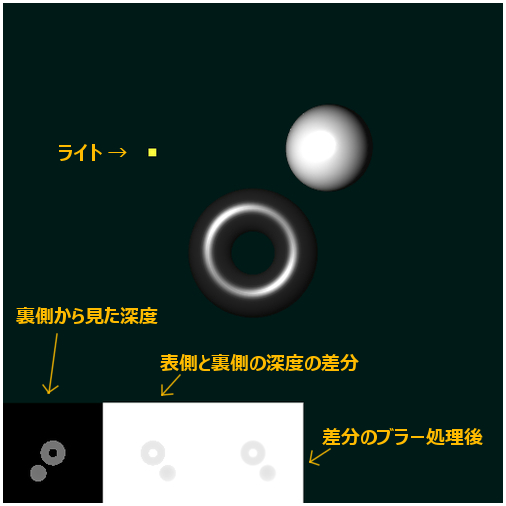
シーンには、トーラスと球体の二つのモデルがレンダリングされます。また、その周辺をぐるりと周回するようにライトが動きます。ライトの位置がわかりやすいように、黄色い点がレンダリングされるようにしてあります。
サンプルの画面の下のほうには、フレームバッファの状態が表示されるようにしてあります。一番左がモデルを裏側から撮影したシーン、左から二番目は深度値の差分、一番右側はそれにブラー処理を施したものです。
これらのことを踏まえてサンプルを動作させてみると、感覚がつかみやすいかもしれませんね。
シェーダの記述
今回はシェーダをなんと六組も使います。ぜいたくですねぇ。
ただし、うち二組はサンプル用に必要なだけなので、実質的には四組のシェーダを使って後光表面下散乱を実装していきます。
第一のシェーダは、最終シーンをレンダリングするシェーダであり、すべてのライティングを一括して受け持つメインシェーダ。
第二のシェーダは、裏側からモデルを見たときの深度値をフレームバッファに描き込む際に利用する深度描き込み用シェーダ。
第三のシェーダは、第二のシェーダを使ってフレームバッファに描き込んだ深度を読み出し、表面と裏面との深度値の差分を算出してからフレームバッファに描き込む差分シェーダ。
第四のシェーダは、第三のシェーダによって描き込まれた深度値の差分をぼかすためのガウシアンブラーシェーダです。
ちなみに、これらの四組のシェーダ以外に、サンプルでは点のレンダリングを行うための頂点シェーダと、フレームバッファの内容を小窓のように合成するための正射影投影用シェーダが含まれます。これで全部で六組のシェーダというわけですね。
深度値を扱う際の精度
以前、シャドウマッピングや被写界深度を扱った際には、深度値を精度高く扱うために RGBA の各要素をフル活用する方法をご紹介したことがありました。
今回のサンプルでは、最終的に深度値の差分に対してブラーを掛けてしまいます。精度の高い深度を用いたところで、結局ぼかしてしまうのであれば恩恵が小さくなってしまいます。また、深度値を RGBA の各要素に分割して高精度な深度値の受け渡しを行う方法は、それなりに負荷の掛かる処理ですので、今回はこれを利用せずに低精度のまま深度を扱っています。
さて、それでは早速ですが、まずは裏面の深度をフレームバッファに描き込む第二のシェーダから見ていきます。
裏面深度値レンダリングシェーダ
// 頂点シェーダ
attribute vec3 position;
uniform mat4 mMatrix;
uniform mat4 mvpMatrix;
uniform vec3 eyePosition;
varying vec4 vColor;
const float near = 0.1;
const float far = 15.0;
const float linerDepth = 1.0 / (far - near);
void main(void){
vec3 pos = (mMatrix * vec4(position, 1.0)).xyz;
float depth = length(eyePosition - pos) * linerDepth;
vColor = vec4(vec3(depth), 1.0);
gl_Position = mvpMatrix * vec4(position, 1.0);
}
// フラグメントシェーダ
precision mediump float;
varying vec4 vColor;
void main(void){
gl_FragColor = vColor;
}カメラの位置と、処理される頂点の位置とを元に深度値をフレームバッファに描き込みます。特に難しいことはしていませんが、定数を使って深度値を正規化しているので自分でプログラムを組むときには気をつけて調整するようにしてください。
続いては、ここで描き込まれた深度を読み出し、差分を計算してフレームバッファに描き込むためのシェーダを見てみましょう。
深度値の差分レンダリングシェーダ
// 頂点シェーダ
attribute vec3 position;
uniform mat4 mMatrix;
uniform mat4 mvpMatrix;
uniform mat4 tMatrix;
uniform vec3 eyePosition;
varying float vDepth;
varying vec4 vTexCoord;
const float near = 0.1;
const float far = 15.0;
const float linerDepth = 1.0 / (far - near);
void main(void){
vec3 pos = (mMatrix * vec4(position, 1.0)).xyz;
vDepth = length(eyePosition - pos) * linerDepth;
vTexCoord = tMatrix * vec4(pos, 1.0);
gl_Position = mvpMatrix * vec4(position, 1.0);
}
// フラグメントシェーダ
precision mediump float;
uniform sampler2D backFaceTexture;
varying float vDepth;
varying vec4 vTexCoord;
void main(void){
float bDepth = 1.0 - texture2DProj(backFaceTexture, vTexCoord).r;
float differnce = 1.0 - clamp(bDepth - vDepth, 0.0, 1.0);
gl_FragColor = vec4(vec3(differnce), 1.0);
}先程と同様の定数値を使って深度値を正規化し、テクスチャから読み出した深度と比較します。
このシェーダでは、以前解説した射影テクスチャマッピングを使ってテクスチャに描き込まれた深度値を読み出しています。ここでは、深度を読み出した後の差分の算出方法に注意が必要です。というのも、テクスチャに描き込まれているのは、裏側に置いたカメラから見た深度です。つまり texture2DProj で読み出した深度は 1.0 から減算することで本来のカメラの位置からの距離になります。
ただしこのままでは厚みが大きいところほど大きな数値になってしまいますので、最終的にはさらに 1.0 から減算することで、光を透過しやすい部分、つまり薄い場所ほど数値が大きくなるようにしてからフレームバッファに描き込むようにします。
さて、続いてはこの深度値の差分、つまり厚みをブラーフィルターによってぼかし処理します。これは以前のテキストで詳細を解説しているのでシェーダのコードのみ掲載しておきます。シェーダ内で使用する weight は、あらかじめ javascript 側で計算しておきシェーダに渡します。
ガウシアンブラーシェーダ
// 頂点シェーダ
attribute vec3 position;
attribute vec2 texCoord;
uniform mat4 ortMatrix;
varying vec2 vTexCoord;
void main(void){
vTexCoord = texCoord;
gl_Position = ortMatrix * vec4(position, 1.0);
}
// フラグメントシェーダ
precision mediump float;
uniform sampler2D texture;
uniform float weight[5];
uniform bool horizontal;
varying vec2 vTexCoord;
const float screenWidth = 512.0;
const float tFrag = 1.0 / screenWidth;
void main(void){
vec2 fc = gl_FragCoord.st;
vec3 destColor = vec3(0.0);
if(horizontal){
destColor += texture2D(texture, (fc + vec2(-4.0, 0.0)) * tFrag).rgb * weight[4];
destColor += texture2D(texture, (fc + vec2(-3.0, 0.0)) * tFrag).rgb * weight[3];
destColor += texture2D(texture, (fc + vec2(-2.0, 0.0)) * tFrag).rgb * weight[2];
destColor += texture2D(texture, (fc + vec2(-1.0, 0.0)) * tFrag).rgb * weight[1];
destColor += texture2D(texture, (fc + vec2( 0.0, 0.0)) * tFrag).rgb * weight[0];
destColor += texture2D(texture, (fc + vec2( 1.0, 0.0)) * tFrag).rgb * weight[1];
destColor += texture2D(texture, (fc + vec2( 2.0, 0.0)) * tFrag).rgb * weight[2];
destColor += texture2D(texture, (fc + vec2( 3.0, 0.0)) * tFrag).rgb * weight[3];
destColor += texture2D(texture, (fc + vec2( 4.0, 0.0)) * tFrag).rgb * weight[4];
}else{
destColor += texture2D(texture, (fc + vec2(0.0, -4.0)) * tFrag).rgb * weight[4];
destColor += texture2D(texture, (fc + vec2(0.0, -3.0)) * tFrag).rgb * weight[3];
destColor += texture2D(texture, (fc + vec2(0.0, -2.0)) * tFrag).rgb * weight[2];
destColor += texture2D(texture, (fc + vec2(0.0, -1.0)) * tFrag).rgb * weight[1];
destColor += texture2D(texture, (fc + vec2(0.0, 0.0)) * tFrag).rgb * weight[0];
destColor += texture2D(texture, (fc + vec2(0.0, 1.0)) * tFrag).rgb * weight[1];
destColor += texture2D(texture, (fc + vec2(0.0, 2.0)) * tFrag).rgb * weight[2];
destColor += texture2D(texture, (fc + vec2(0.0, 3.0)) * tFrag).rgb * weight[3];
destColor += texture2D(texture, (fc + vec2(0.0, 4.0)) * tFrag).rgb * weight[4];
}
gl_FragColor = vec4(vec3(1.0) - destColor, 1.0);
}さて、かなり長くなってしまいますが最後にメインシェーダを見てみます。
メインシェーダでは、通常のライティングの計算のほか、ブラー処理を行った深度値の差分を読み出してモデルの厚みを元に透過してくる色の強さを決定します。
最終シーン用のメインシェーダ
// 頂点シェーダ
attribute vec3 position;
attribute vec3 normal;
attribute vec4 color;
uniform mat4 mMatrix;
uniform mat4 mvpMatrix;
uniform mat4 invMatrix;
uniform mat4 tMatrix;
uniform vec3 lightPosition;
uniform vec3 eyes;
uniform vec3 eyePosition;
uniform vec4 ambientColor;
varying vec4 vColor;
varying vec4 vTexCoord;
varying float vDotLE;
void main(void){
vec3 pos = (mMatrix * vec4(position, 1.0)).xyz;
vec3 invLight = normalize(invMatrix * vec4(lightPosition - pos, 0.0)).xyz;
vec3 invEye = normalize(invMatrix * vec4(eyePosition, 0.0)).xyz;
vec3 halfLE = normalize(invLight + invEye);
float diffuse = clamp(dot(normal, invLight), 0.0, 1.0);
float specular = pow(clamp(dot(normal, halfLE), 0.0, 1.0), 50.0);
vColor = color * vec4(vec3(diffuse), 1.0) + vec4(vec3(specular), 0.0) + ambientColor;
vTexCoord = tMatrix * vec4(pos, 1.0);
vDotLE = pow(max(dot(normalize(eyes - eyePosition), normalize(lightPosition)), 0.0), 10.0);
gl_Position = mvpMatrix * vec4(position, 1.0);
}
// フラグメントシェーダ
precision mediump float;
uniform sampler2D blurTexture;
varying vec4 vColor;
varying vec4 vTexCoord;
varying float vDotLE;
const vec3 throughColor = vec3(1.0, 0.5, 0.2);
void main(void){
float bDepth = pow(texture2DProj(blurTexture, vTexCoord).r, 20.0);
vec3 through = throughColor * vDotLE * bDepth;
gl_FragColor = vec4(vColor.rgb + through, vColor.a);
}ここでポイントになる部分を抜粋して説明します。
まず頂点シェーダには、通常のグーローシェーディングによるライティング処理が入りますので、当サイトではおなじみの各種 uniform 変数が入ってきます。そして main 関数の内部で varying 変数 vColor に代入を行っている部分までは、この通常のライティング処理を行っている部分です。
さらにその下、varying 変数 vTexCoord にはテクスチャ座標が、そして vDotLE には視線とライトベクトルがどの程度向き合っているのかの係数が入り、フラグメントシェーダに渡されます。
テクスチャ座標の算出と、視線とライトベクトルの係数算出
vTexCoord = tMatrix * vec4(pos, 1.0);
vDotLE = pow(max(dot(normalize(eyes - eyePosition), normalize(lightPosition)), 0.0), 10.0);一方、フラグメントシェーダ側では、定数を使って表面下散乱で透過されてくる色を指定して利用しています。それが throughColor ですね。フラグメントシェーダの main 関数の内部で、まずは float 型の変数 bDepth に射影テクスチャマッピングを使って深度値を読み出し、その結果を throughColor などと乗算します。
読み出した深度値は、今回のサンプルの場合そのままではかなり大きな数値になってしまうことが多いため、GLSL の組み込み関数である pow を使って補正しています。
こうして、長い長いシェーダの旅を終え、やっとひとつのフラグメントに色が描き込まれます。文章にして解説すると本当に冗長ですが、これがリアルタイムで動作するのですから今更ながら驚きます。
javascript 側のプログラム
さて、まだ終わりません。続いて、メインプログラムとなる javascript 側の処理を解説します。
今回のサンプルで特に難しく紛らわしい部分としては、ビュー×プロジェクション座標変換行列などの、多数の行列をうまく使い分けなければならない点が挙げられます。
最終的にレンダリングされるシーンは、透視投影による座標変換が行われた結果になります。つまりわかりやすく言ってしまえば、遠くにあるものは小さく手前にあるものは大きくという遠近感のある仕上がりになるということです。
しかしここで考えてみてほしいのですが、表面と裏面とを両方レンダリングする今回のサンプル。もし、裏面や表面の深度をフレームバッファに描き込む際に、最終シーンと同様に遠近法が適用されたレンダリングを行うとどうなるでしょうか。
答えから言ってしまうと、正しく表面下散乱がレンダリングできません。これはなぜかと言うと、モデルの裏側にカメラを置き裏面の深度をレンダリングする場面では、当然と言えば当然ですが、本来のカメラより遠い位置にあるモデルはバッファ上で大きなサイズでレンダリングされてしまいますね。一方、本来のカメラ見ると、そのモデルはバッファ上で小さなサイズでレンダリングされるはずです。
この裏側のカメラから見た場合と、本来のカメラから見た場合との、スクリーン上でのモデルの大きさの違いが深度の差分を計算する場面で問題を起こします。これを無視して無理やりレンダリングした結果が以下のような状態です。
深度の描き込みに透視変換を用いた場合の結果

ご覧のとおり、裏側のカメラと本来のカメラで、サイズに差異が生まれた部分が色の歪みとなって表れてしまっていますね。これでは正しく深度値の差分を計算できません。
そこで登場するのが正射影変換です。透視変換と違い、正射影変換では遠くにあるものでも近くにあるものでも、本来のサイズでしかレンダリングされません。言い換えれば、遠近法が適用されない状態になるということです。この正射影変換の特性をうまく利用することで、裏と表の両方のカメラで、同じサイズのモデルとして比較することができるのですね。
ただし、ただ単に正射影変換を行えばいいかと言うと、実はそうではないんです。ここがまたややこしいところ。
よくよく考えてみれば当たり前のことですが、裏側に置かれたカメラから見える世界は、本来のカメラで捉えた世界を鏡に映したように左右が反転しています。本来のカメラから見て左側にあるはずのモデルは、裏側から見れば右側に置かれてしまっているわけです。
つまり、深度値の差分を算出する際には、どこかのタイミングで左右反転した座標を参照できるようにしてやる必要があります。今回のサンプルでは、シェーダではなくメインプログラムのほうでこの左右反転の処理を入れています。
具体的には、差分を検出するシェーダに渡す射影テクスチャ用の行列を、あらかじめ X 軸のみ反転した状態で掛け合わせておくようにします。
かなり紛らわしいのでコードを掲載して見てみます。
行列生成のあれこれ
// 最終シーンで使う透視射影変換行列の生成(tmpMatrix) ※ 1
m.lookAt(eyePosition, eyes, camUpDirection, vMatrix);
m.perspective(45, c.width / c.height, 0.1, 15, pMatrix);
m.multiply(pMatrix, vMatrix, tmpMatrix);
// バックバッファに描き込む際に使用する正射影変換行列の生成(ort_tmpMatrix) ※ 2
m.ortho(-3.0, 3.0, 3.0, -3.0, 0.1, 15, ort_pMatrix);
m.multiply(ort_pMatrix, vMatrix, ort_tmpMatrix);
// 裏面の深度値を描き込む際に使用する正射影変換行列の生成(inv_ort_tmpMatrix) ※ 3
m.lookAt(invEyePosition, eyes, camUpDirection, inv_vMatrix);
m.multiply(ort_pMatrix, inv_vMatrix, inv_ort_tmpMatrix);
// テクスチャ座標変換用の行列を掛け合わせておく ※ 4
tMatrix[0] = 0.5;
m.multiply(tMatrix, ort_pMatrix, tvpMatrix);
m.multiply(tvpMatrix, vMatrix, tmvpMatrix);
// テクスチャ座標変換用の行列を掛け合わせておく(X軸反転版) ※ 5
tMatrix[0] = -0.5;
m.multiply(tMatrix, ort_pMatrix, tvpMatrix);
m.multiply(tvpMatrix, vMatrix, itmvpMatrix);ここで登場する変数 m は、当サイトのオリジナルライブラリ minMatrix.js を用いて生成できる matIV オブジェクトです。
まず最終シーン用の、いわゆる遠近感のあるシーンを作るためのビュー×プロジェクション座標変換行列(※ 1)が、上記で言うと tmpMatrix に入ります。これはいつもどおりの処理です。
そして、フレームバッファに正射影で描き込むためのビュー×プロジェクション座標変換行列(※ 2)が ort_tmpMatrix になります。これには matIV オブジェクトの ortho メソッドが使われているのがわかると思います。
さらに裏面を描き込むための座標変換行列(※ 3)である inv_ort_tmpMatrix も用意しておきます。ここでは lookAt メソッドに渡す第一引数に、原点に点対称なカメラの位置( invEyePosition )を渡していますね。原点に点対称な位置にカメラを置くことで、モデルを向こう側から眺めるカメラができあがるという寸法です。
続く※ 4 と※ 5 では、テクスチャ座標変換用の行列を準備していますが、先述のとおり X 軸を反転させた行列をあらかじめ準備しておくのがポイントです。裏面の深度値を読み出す際に、この X 軸反転版の行列を使うことで正しく差分を計算できます。
あとは、それぞれのシーンで適切にシェーダを選択し、適切に行列やパラメータをシェーダに送ってやれば OK です。と、言葉で言うのは簡単ですが、コードでみると結構な文量になります。ここは焦らず、じっくりとコードを読み解くことをオススメします。
まとめ
さて、恐ろしく長いテキストになってしまいましたが、理解できたでしょうか。
今回のサンプルは、今まで解説してきたテキストの内容を流用、応用したものでしかありません。概念的な部分は、すでに別のサンプルで詳細に解説しています。しかし、それらを複雑に組み合わせることで、最終的には独特な効果を生み出すことが可能になります。
冒頭でも書きましたが、表面下散乱には用途や目的に合わせて様々な手法があります。そして、それぞれの手法によって実装方法も、また最終的に生み出される結果もまるで違ったものになってきます。
今回のサンプルは、表面下散乱という言葉こそ使っているものの、実際には[ 後光透過シェーダ ]とでも名づけたほうがいいものなのかもしれません。しかし、モデルの裏側から当たったライトの光がブラー処理によってぼかされ、ぼんやりと透過して見える様はまさに表面下散乱そのもの。手のひらを太陽にかざしたときのように、光が透けて見えるモデルをレンダリングすることができる今回のサンプルは、まがりなりにも表面下散乱の一種だと個人的には思います。
実に四組ものシェーダを使い、さらに5パスで最終シーンができあがるかたちになりますので、そんなにコストの安い実装ではありません。使いどころは限定されるかもしれませんが、光を透過するような半透明物体をリアルに表現したい場合には、参考になるのではないでしょうか。
今回のサンプルも実際に動作するものを見たい場合には以下にリンクがあります。動作するサンプルを参考に、がんばって取り組んでみてください。
