シャドウマッピング

影の描画

前回は射影テクスチャマッピングを応用したテクニックのひとつとして、光学迷彩を取り上げました。光学迷彩を施すモデルの後ろにあるものは全て事前にレンダリングする必要があるため、コストはけして安くないものの、その見た目のかっこよさは今までのサンプルのなかでもピカイチだったのではないでしょうか。

さて、今回は影のレンダリングに挑戦します。

とは言え、影をレンダリングするための手法には様々なものが考案されており、それぞれにメリットとデメリットがあります。今回やってみるのはモデルの深度値を格納するデプスバッファを使った、一般にデプスバッファシャドウなどと呼ばれている手法です。

深度値を用いたシャドウマッピングでは、次のような手順でモデルをレンダリングしていきます。

• オフスクリーン用のフレームバッファを用意
• フレームバッファにライトから見たときの深度値を描き込む
• 本番のレンダリングでフレームバッファの深度値を読み出す
• 読み出した深度値とレンダリングする頂点の深度を比較する
• 比較結果をもとに影を描画するかどうか決定する

まず前提として、フレームバッファによるオフスクリーンレンダリングを使う必要があります。今までは、フレームバッファには普通にモデルをレンダリングしていました。しかし今回はここにライトから見たときの深度値のみを描き込みます。

深度値のみを描き込むという意味がわからない人もいるかもしれませんが、要は、オフスクリーンのフレームバッファに、ライトから見たときのデプスバッファの情報をまるまる残しておくようにするのが目的です。オフスクリーンのフレームバッファは、テクスチャを正しくアタッチしてあれば当然あとからその内容をフラグメントシェーダの内部で参照することが可能になります。本番のレンダリングを行なう際に、フレームバッファから読み出した深度値と、実際にレンダリングしようとしている頂点の深度を比較すれば、その頂点が影にあるのかどうかを判別できるというわけです。

若干わかりにくい部分もあると思いますので、次項からさらにじっくりと見ていきましょう。

デプスバッファに書き込まれている情報

そもそも、デプスバッファ(深度バッファ)とはどんな役割を持つバッファだったか憶えているでしょうか。

デプスバッファは、深度テスト( Z テスト)を行なう際などに利用されるバッファで、頂点の深度にかかわる情報を保持しています。次々とモデルが描画されていく際に、奥にあるものは手前にあるものによって遮られ隠れるという、現実世界では当たり前のように起こる現象を再現するためにデプスバッファは欠かせない存在です。

デプスバッファに書き込まれているのは、あくまでも深度です。さらに、その範囲は 0.0 ～ 1.0 の範囲に必ず収まるようになっています。カメラに最も近いところは 0.0 に、最も遠いところが 1.0 になるわけですね。

フレームバッファに深度値を描き込む際には、この 0.0 ～ 1.0 の範囲の値を描き込むことになります。このとき重要なのは、フレームバッファに描き込む深度値はライトから見たときの深度値であるという点です。

影は、光のないところには落ちません。当然ですが、カメラがあっただけで影が落ちるなんてこともありません。ライトがあるからこそ影が落ちるのです。ですから、フレームバッファに描き込む深度値はライトの位置を視点として見たときの各頂点の深度値ということになります。

深度値を読み出す

フレームバッファに深度値を描き込んだあと、実際にそれを読み出すときも注意が必要です。

先ほども書いたように、フレームバッファに描き込まれているのはあくまでもライトから見たときの深度です。ですから、深度値を比較するためにはシェーダに対してカメラから見たときの通常の座標変換行列の他に、ライトから見たときの座標変換行列を送ってやる必要があります。シェーダの内部では、実際にレンダリングを行なうためのカメラ視点の座標変換と、ライトから見たときの座標変換とを同時に行なうことになります。

深度値を読み出す際には、以前のテキストで解説した射影テクスチャマッピングを用います。フラグメントシェーダの内部で texture2DProj を使って深度値を読み出し、ライト視点で座標変換した頂点の深度値と比較を行ないます。

このときフレームバッファから読み出した深度が仮に 0.5 であったとします。深度値は奥にあればあるほど 1.0 に近づいていくわけですから、この 0.5 という深度値よりも大きな数値を持つ頂点は、手前になにかしらのモデルが存在していることになりますね。

ライト視点で考えたときの深度

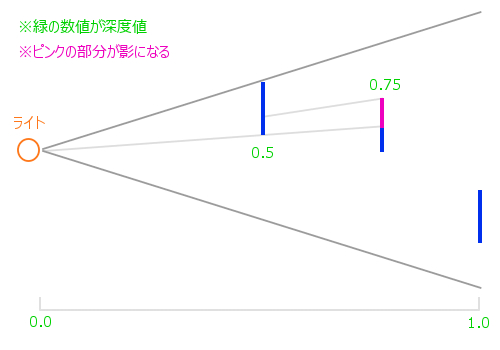
このように、ライト視点で見たときの深度を使って、どのフラグメントが影になるかを判断します。基本的に影になるかどうかは真偽値で決まりますので、仮に影になる場合には対象のフラグメントの色を減算してやればいいわけですね。

深度値を正しく橋渡しする

さて、ここまで長々と書いてきましたが、デプスバッファシャドウには非常に大きな弱点があります。

それは深度値を橋渡しするための役割を担うフレームバッファのテクスチャです。

なぜテクスチャが弱点になってしまうのか……。それは、テクスチャに格納できる値の精度に関係しています。

よく考えてみればわかることですが、テクスチャに描き込まれる色は RGB がそれぞれ 0 ～ 255 までの 256 諧調です。つまり、これを言い換えるとテクスチャには 8 ビットの精度しかないということでもありますね。※ここではバイトやビットに関する解説はしませんので、ビットとはなんぞやという人は各自きちんと調べてください。

デプスバッファに格納されている値は、当然 8 ビットよりも精度の高い数値です。これをテクスチャに書き込んでしまうと、最大でも 8 ビットで表現できる範囲でしか深度値を保存することができなくなってしまいます。表現できない部分の数値は丸められ、本来の深度値とは異なる数値を参照しなければならなくなってしまいます。

しかし、ここで考えてみてください。

テクスチャには、RGBA の四つの要素を使って色を書き込むことができます。一つ一つの要素は 8 ビットの精度しか持っていませんが、それが四つ分あるとすると 8 x 4 = 32 で、32 ビット分のデータ領域が存在することがわかりますね。

テクスチャに深度値を描き込む際、一つの 8 ビット分の領域を使うのではなく、残っている 24 ビット分のデータ領域も活用することができれば、テクスチャを媒体とした精度の高い数値の受け渡しができるようになります。メールにファイルを添付する際に、ファイルを圧縮し受け取り先で解凍するのと同じように、フレームバッファに描き込む深度値を 32 ビットに変換してから描き込み、読み出しする際に元の深度値を復元するような仕組みが作れれば、高い精度の深度値を複数のシェーダでやり取りすることが可能になります。

これを実現するには、深度値を特殊な計算方法によって四つの要素に分解する処理が必要です。

まず、本来の深度値を 255 倍してその小数点以下の数値だけを抜き出します。そして、そこで抜き出された小数点以下の数値をまた 255 倍してから、小数点以下の数値だけを抜き出します。これを繰り返して RGBA のそれぞれの値に格納していきます。

こうして深度値を分解することができたら誤差を相殺するためのバイアスを各要素にかけてやります。

バイアスは 1 を 255 で割った数値を用い、次のように計算しておきます。

ここまで計算できたら、その数値を RGBA の各要素の値としてフレームバッファに描き込んでおきます。フレームバッファから深度値を読み出したら、RGBA の各要素を今度は先ほどとは逆の手順で展開してやります。

このように 32 ビット分をフルに使って深度値をやり取りすることで、本来のテクスチャの色要素として格納できるビット精度と比べ、4 倍もの精度を持つ値の橋渡しが可能です。

ちょっとわかりにくい概念かもしれませんが、今回のサンプルでもシェーダ内でこれに相当する処理を行なっていますので、最低限、そのことだけは理解しておいてください。

フレームバッファへの描き込み

前回の光学迷彩もなかなかのコード量でしたが、今回もそれなりにソースコードが長いです。ポイントを絞って理解していってください。

まずは、シェーダのソースから見てみようと思いますが、今回のサンプルではシェーダを二組用意して使い分けます。

一つ目のシェーダは、フレームバッファに深度を描き込むためのシェーダです。二つ目のシェーダは実際にスクリーンにレンダリングを行なう際に利用するシェーダですね。

まず最初はフレームバッファに深度を描き込むためのシェーダです。

深度値格納用：頂点シェーダ

attribute vec3 position;
uniform   mat4 mvpMatrix;

varying   vec4 vPosition;

void main(void){
	vPosition = mvpMatrix * vec4(position, 1.0);
	gl_Position = vPosition;
}

深度値格納用：フラグメントシェーダ

precision mediump float;

uniform bool depthBuffer;

varying vec4 vPosition;

vec4 convRGBA(float depth){
	float r = depth;
	float g = fract(r * 255.0);
	float b = fract(g * 255.0);
	float a = fract(b * 255.0);
	float coef = 1.0 / 255.0;
	r -= g * coef;
	g -= b * coef;
	b -= a * coef;
	return vec4(r, g, b, a);
}

void main(void){
	vec4 convColor;
	if(depthBuffer){
		convColor = convRGBA(gl_FragCoord.z);
	}else{
		float near = 0.1;
		float far  = 150.0;
		float linerDepth = 1.0 / (far - near);
		linerDepth *= length(vPosition);
		convColor = convRGBA(linerDepth);
	}
	gl_FragColor = convColor;
}

まずは頂点シェーダですが、こちらはご覧のとおり、特別なことはやってません。ただ単に、座標変換行列を使って頂点座標を変換しているだけです。ポイントは varying 変数としてフラグメントシェーダに頂点情報を送っていることくらいです。

ちょっと難しいのはフラグメントシェーダのほうですね。

こちらでは、先ほど解説した RGBA に深度値を分解して格納する処理が入っています。深度値を 32 ビット精度に変換するための関数 convRGBA がシェーダ内で定義されているのがわかると思います。

しかしフラグメントシェーダにはもう一つ重要なポイントが隠されています。それは uniform 変数として入ってくる変数 depthBuffer の使い方です。これはシェーダのソースを見るとわかるとおり真偽値です。この真偽値を使って処理を分岐している箇所を見ると convRGBA に渡す値の種類が変わっていることがわかると思います。

uniform 変数 depthBuffer が真の場合に登場する gl_FragCoord は GLSL の組み込み変数で、デプスバッファの深度値をそのまま拾ってきてくれます。

一方、uniform 変数 depthBuffer が偽だった場合には、頂点の座標位置を使って何かしらの計算を行なっているのがわかると思います。こちらは、デプスバッファの深度値を使うのではなく、頂点座標からダイレクトに深度に相当する値を生成してフラグメントに描き込んでいます。

今回のサンプルでは、デプスバッファの値を使った深度値の比較と、ダイレクトに座標位置を使って比較する場合とを、HTML に埋め込んだ input 要素から選択できるようにしています。これは実際にサンプルを動作させるとわかると思いますが、概ね、ダイレクトに頂点座標を使った場合のほうが精度の高い影生成を行うことができます。

コードを比較すればわかるとおり、デプスバッファを使った場合のほうがはるかに処理としては簡素です。負荷とのトレードオフになりますが、場面によって使い分けできるように今回のサンプルではどちらもできるようにコードを書きました。

スクリーンへのレンダリング

深度値をフレームバッファに描き込むことができたら、今度はこれを読み出して比較するためのシェーダが必要になりますね。

こちらもまずは頂点シェーダから見ていきます。

スクリーンレンダリング用：頂点シェーダ

attribute vec3 position;
attribute vec3 normal;
attribute vec4 color;
uniform   mat4 mMatrix;
uniform   mat4 mvpMatrix;
uniform   mat4 tMatrix;
uniform   mat4 lgtMatrix;
varying   vec3 vPosition;
varying   vec3 vNormal;
varying   vec4 vColor;
varying   vec4 vTexCoord;
varying   vec4 vDepth;

void main(void){
	vPosition   = (mMatrix * vec4(position, 1.0)).xyz;
	vNormal     = normal;
	vColor      = color;
	vTexCoord   = tMatrix * vec4(vPosition, 1.0);
	vDepth      = lgtMatrix * vec4(position, 1.0);
	gl_Position = mvpMatrix * vec4(position, 1.0);
}

今回のサンプルでは、影の生成のほかに点光源によるライティングを行ないます。その都合上、いくつかの varying 変数が登場していますが、ポイントとなるのは vTexCoord と vDepth の二つの varying 変数です。

頂点シェーダ内に入ってくる uniform 変数はいずれも行列で、このうち vTexCoord に入る値にはテクスチャ変換用の行列である tMatrix が使われます。これは影を射影テクスチャマッピングによって投影するために必要になります。

一方 vDepth に入る値にはライト視点での座標変換行列で変換した頂点座標が入ります。uniform 変数 lgtMatrix には、ライトから見た場合の mvpMatrix に相当する行列が送られてくるようにメインプログラムを組みます。

各行列の意味

さて、続いてはフラグメントシェーダです。こちらは結構長いコードになりますが、臆せず見ていきましょう。

スクリーンレンダリング用：フラグメントシェーダ

precision mediump float;

uniform mat4      invMatrix;
uniform vec3      lightPosition;
uniform sampler2D texture;
uniform bool      depthBuffer;
varying vec3      vPosition;
varying vec3      vNormal;
varying vec4      vColor;
varying vec4      vTexCoord;
varying vec4      vDepth;

float restDepth(vec4 RGBA){
	const float rMask = 1.0;
	const float gMask = 1.0 / 255.0;
	const float bMask = 1.0 / (255.0 * 255.0);
	const float aMask = 1.0 / (255.0 * 255.0 * 255.0);
	float depth = dot(RGBA, vec4(rMask, gMask, bMask, aMask));
	return depth;
}

void main(void){
	vec3  light     = lightPosition - vPosition;
	vec3  invLight  = normalize(invMatrix * vec4(light, 0.0)).xyz;
	float diffuse   = clamp(dot(vNormal, invLight), 0.2, 1.0);
	float shadow    = restDepth(texture2DProj(texture, vTexCoord));
	vec4 depthColor = vec4(1.0);
	if(vDepth.w > 0.0){
		if(depthBuffer){
			vec4 lightCoord = vDepth / vDepth.w;
			if(lightCoord.z - 0.0001 > shadow){
				depthColor  = vec4(0.5, 0.5, 0.5, 1.0);
			}
		}else{
			float near = 0.1;
			float far  = 150.0;
			float linerDepth = 1.0 / (far - near);
			linerDepth *= length(vPosition.xyz - lightPosition);
			if(linerDepth - 0.0001 > shadow){
				depthColor  = vec4(0.5, 0.5, 0.5, 1.0);
			}
		}
	}
	gl_FragColor = vColor * vec4(vec3(diffuse), 1.0) * depthColor;
}

フラグメントシェーダ内では、フレームバッファに描き込んだ 32 ビットの深度値を本来の値に変換しなおすための関数 restDepth が定義されています。また main 関数の上から三行目までは、点光源による拡散光のライティング計算を行なっています。

メイン処理のなかの四行目では texture2DProj を使って、フレームバッファに描き込まれた深度値を読み出し、それを restDepth 関数によって再変換していますね。ここで得られた変数 shadow の値が復元された深度値になります。

フレームバッファへ深度値を描き込むときと同様、こちらのシェーダでも uniform 変数として入ってきた depthBuffer という真偽値に応じて処理を分岐しています。

フレームバッファへの描き込み時にデプスバッファの値を使った場合には、ライト視点で見たときの座標変換を行なった頂点の Z 値と、変数 shadow の値を比較します。ここで登場する 0.0001 という数字は深度値が完全に一致した場合に、マッハバンドと呼ばれる縞模様が発生してしまうことを避けるための措置です。

uniform 変数 depthBuffer が偽だった場合、つまりフレームバッファの描き込みにダイレクトに頂点位置を用いた場合では、こちらのシェーダ内部でも同じように頂点座標をもとに変換を行い、読み出した深度値と比較します。

いずれにしても、対象のフラグメントが影になると判断できた場合には色を減算する処理へ移るようになっているのがわかると思います。

やっとメインプログラム

さて、シェーダの解説だけで相当長くなりました。メインプログラムとなる javascript のほうもめげずに見ていきます。

今回のサンプルでは、先述のとおり二種類のシェーダプログラムを使い分けます。また、フレームバッファへのオフスクリーンレンダリングを行うことになりますので、これらの点に注意しながらコードを記述していきます。

二種類のシェーダ

// 頂点シェーダとフラグメントシェーダからプログラムオブジェクトを生成
var v_shader = create_shader('svs');
var f_shader = create_shader('sfs');
var prg = create_program(v_shader, f_shader);

// 同上(シャドウマップ用)
v_shader = create_shader('dvs');
f_shader = create_shader('dfs');
var dPrg = create_program(v_shader, f_shader);

上記のコードが二つのシェーダを用意している部分です。若干似たような名前をつけてしまったのでわかりにくいかもしれませんが、変数 prg が最終的にスクリーンにレンダリングを行なうシェーダ。変数 dPrg がフレームバッファに深度値を描き込むためのシェーダです。

恒常ループ

// 恒常ループ
(function(){
	// カウンタをインクリメントする
	count++;
	
	// ビュー×プロジェクション座標変換行列
	var eyePosition = new Array();
	var camUpDirection = new Array();
	q.toVecIII([0.0, 70.0, 0.0], qt, eyePosition);
	q.toVecIII([0.0, 0.0, -1.0], qt, camUpDirection);
	m.lookAt(eyePosition, [0, 0, 0], camUpDirection, vMatrix);
	m.perspective(45, c.width / c.height, 0.1, 150, pMatrix);
	m.multiply(pMatrix, vMatrix, tmpMatrix);
	
	// テクスチャ変換用行列
	m.identity(tMatrix);
	tMatrix[0]  = 0.5; tMatrix[1]  = 0.0; tMatrix[2]  = 0.0; tMatrix[3]  = 0.0;
	tMatrix[4]  = 0.0; tMatrix[5]  = 0.5; tMatrix[6]  = 0.0; tMatrix[7]  = 0.0;
	tMatrix[8]  = 0.0; tMatrix[9]  = 0.0; tMatrix[10] = 1.0; tMatrix[11] = 0.0;
	tMatrix[12] = 0.5; tMatrix[13] = 0.5; tMatrix[14] = 0.0; tMatrix[15] = 1.0;
	
	// ライトの距離をエレメントの値に応じて調整
	var r = eRange.value;
	lightPosition[0] = 0.0 * r;
	lightPosition[1] = 1.0 * r;
	lightPosition[2] = 0.0 * r;
	
	// ライトから見たビュー座標変換行列
	m.lookAt(lightPosition, [0, 0, 0], lightUpDirection, dvMatrix);
	
	// ライトから見たプロジェクション座標変換行列
	m.perspective(90, 1.0, 0.1, 150, dpMatrix);
	
	// テクスチャ座標変換用行列
	m.multiply(tMatrix, dpMatrix, dvpMatrix);
	m.multiply(dvpMatrix, dvMatrix, tMatrix);
	
	// ライトから見たビュー×プロジェクション座標変換行列
	m.multiply(dpMatrix, dvMatrix, dvpMatrix);
	
	// 深度値比較のタイプをエレメントから取得
	var t = eRadio.checked;
	
	// プログラムオブジェクトの選択(シャドウマップ用)
	gl.useProgram(dPrg);
	
	// フレームバッファをバインド
	gl.bindFramebuffer(gl.FRAMEBUFFER, fBuffer.f);
	
	// フレームバッファを初期化
	gl.clearColor(1.0, 1.0, 1.0, 1.0);
	gl.clearDepth(1.0);
	gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
	
	// トーラスの描画(合計10個)
	set_attribute(dtVBOList, dAttLocation, dAttStride);
	gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, tIndex);
	for(var i = 0; i < 10; i++){
		var rad = ((count + i * 36) % 360) * Math.PI / 180;
		var rad2 = (((i % 5) * 72) % 360) * Math.PI / 180;
		var ifl = -Math.floor(i / 5) + 1;
		m.identity(mMatrix);
		m.rotate(mMatrix, rad2, [0.0, 1.0, 0.0], mMatrix);
		m.translate(mMatrix, [0.0, ifl * 10.0 + 10.0, (ifl - 2.0) * 7.0], mMatrix);
		m.rotate(mMatrix, rad, [1.0, 1.0, 0.0], mMatrix);
		m.multiply(dvpMatrix, mMatrix, lgtMatrix);
		gl.uniformMatrix4fv(dUniLocation[0], false, lgtMatrix);
		gl.uniform1i(dUniLocation[1], t);
		gl.drawElements(gl.TRIANGLES, torusData.i.length, gl.UNSIGNED_SHORT, 0);
	}
	
	// 板ポリゴンの描画(底面)
	set_attribute(dvVBOList, dAttLocation, dAttStride);
	gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, vIndex);
	m.identity(mMatrix);
	m.translate(mMatrix, [0.0, -10.0, 0.0], mMatrix);
	m.scale(mMatrix, [30.0, 0.0, 30.0], mMatrix);
	m.multiply(dvpMatrix, mMatrix, lgtMatrix);
	gl.uniformMatrix4fv(dUniLocation[0], false, lgtMatrix);
	gl.drawElements(gl.TRIANGLES, index.length, gl.UNSIGNED_SHORT, 0);
	
	// プログラムオブジェクトの選択
	gl.useProgram(prg);
	
	// フレームバッファのバインドを解除
	gl.bindFramebuffer(gl.FRAMEBUFFER, null);
	
	// フレームバッファをテクスチャとしてバインド
	gl.activeTexture(gl.TEXTURE0);
	gl.bindTexture(gl.TEXTURE_2D, fBuffer.t);
	
	// canvasを初期化
	gl.clearColor(0.0, 0.7, 0.7, 1.0);
	gl.clearDepth(1.0);
	gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
	
	// トーラスの描画(合計10個)
	set_attribute(tVBOList, attLocation, attStride);
	gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, tIndex);
	for(i = 0; i < 10; i++){
		rad = ((count + i * 36) % 360) * Math.PI / 180;
		rad2 = (((i % 5) * 72) % 360) * Math.PI / 180;
		ifl = -Math.floor(i / 5) + 1;
		m.identity(mMatrix);
		m.rotate(mMatrix, rad2, [0.0, 1.0, 0.0], mMatrix);
		m.translate(mMatrix, [0.0, ifl * 10.0 + 10.0, (ifl - 2.0) * 7.0], mMatrix);
		m.rotate(mMatrix, rad, [1.0, 1.0, 0.0], mMatrix);
		m.multiply(tmpMatrix, mMatrix, mvpMatrix);
		m.inverse(mMatrix, invMatrix);
		m.multiply(dvpMatrix, mMatrix, lgtMatrix);
		gl.uniformMatrix4fv(uniLocation[0], false, mMatrix);
		gl.uniformMatrix4fv(uniLocation[1], false, mvpMatrix);
		gl.uniformMatrix4fv(uniLocation[2], false, invMatrix);
		gl.uniformMatrix4fv(uniLocation[3], false, tMatrix);
		gl.uniformMatrix4fv(uniLocation[4], false, lgtMatrix);
		gl.uniform3fv(uniLocation[5], lightPosition);
		gl.uniform1i(uniLocation[6], 0);
		gl.uniform1i(uniLocation[7], t);
		gl.drawElements(gl.TRIANGLES, torusData.i.length, gl.UNSIGNED_SHORT, 0);
	}
	
	// 板ポリゴンの描画
	set_attribute(vVBOList, attLocation, attStride);
	gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, vIndex);
	m.identity(mMatrix);
	m.translate(mMatrix, [0.0, -10.0, 0.0], mMatrix);
	m.scale(mMatrix, [30.0, 0.0, 30.0], mMatrix);
	m.multiply(tmpMatrix, mMatrix, mvpMatrix);
	m.inverse(mMatrix, invMatrix);
	m.multiply(dvpMatrix, mMatrix, lgtMatrix);
	gl.uniformMatrix4fv(uniLocation[0], false, mMatrix);
	gl.uniformMatrix4fv(uniLocation[1], false, mvpMatrix);
	gl.uniformMatrix4fv(uniLocation[2], false, invMatrix);
	gl.uniformMatrix4fv(uniLocation[3], false, tMatrix);
	gl.uniformMatrix4fv(uniLocation[4], false, lgtMatrix);
	gl.drawElements(gl.TRIANGLES, index.length, gl.UNSIGNED_SHORT, 0);
	
	// コンテキストの再描画
	gl.flush();
	
	// ループのために再帰呼び出し
	setTimeout(arguments.callee, 1000 / 30);
})();

恒常ループの中身だけを抜粋したんですが、それでも結構な行数がありますね。

やっていることを簡単に列挙すると……フレームバッファをバインドし、ライトを視点としてレンダリングを行なう。さらに、フレームバッファのバインドを解除し、スクリーンへレンダリングを行なう。というだけのことなんですが、どうしても WebGL をスクラッチで書くと冗長になりますね。

レンダリングされるトーラスは全部で 10 個あります。上段・下段にそれぞれ 5 個ずつ、五角形の頂点位置に配するような形で並びます。そのほか、床を表現するために板状のポリゴンを一枚レンダリングするようになっています。

まとめ

随分長いテキストになりましたが、シャドウマッピング、いかがでしたでしょうか。

影に関する処理は、今でもいろいろな手法が研究・開発されています。そのなかでも、今回紹介したシャドウマッピングは比較的ポピュラーな部類でしょう。

ただし、サンプルを動作させてもらえればわかると思いますが、意外と影の精度が上がりません。デプスバッファの値ではなく、ダイレクトに頂点座標を使った場合のほうが若干マシな感じもするのですが、これは動作環境などによっても変わってくる可能性があります。

正直なところ、実装はできましたがこれを実用化するとなると非常に細かな調整が必要になると思います。ライトとモデルの距離、影を描画することによるボトルネックなど、対応しなければならない問題はけして少なくありません。

また、今回のサンプルでは影が非常にデコボコとした状態になっています。これには解決方法があるのですが、その話はまた次回にしようと思います。

サンプルは以下にリンクがありますので、実際に動作するものを見ることができます。サンプルではライトの距離を調整できるほか、デプスバッファの値を使うか使わないか、ラジオボタンで選択できるようになっています。

@h_doxas Twitter