リムライティング

今回のサンプルの実行結果
浮かび上がるシルエット
前回は半球ライティングを解説しました。半球ライティングは環境光のライティングを発展させたような技術で、天空色と、照り返しによる地面の色とが自然と混ざり合うような照明効果が得られるのでしたね。
半球ライティングは計算の負荷もそれほど高くなく、その割には自然な照明効果が得られるため状況に応じて使ってみていただければと思います。
さて、今回は前回に引き続き照明系を扱いたいと思います。今回はリムライティングです。
リムライティングは、主にモデルの後方からライトが当たっている状態を再現する照明効果で、モデルの後方から来たライトの光が、モデルの輪郭部分にうっすらと露光している状態をシミュレートします。こうして言葉で書いてみると少々わかりにくいかもしれませんが、以下の画像を見るとなんとなくどういう意味かわかるのではないでしょうか。
リムライティングの例

この画像のように背景が真っ暗なシーンのほか、強い太陽の光が降り注ぐ朝方の屋外シーンなど、リムライティングが有効に活用できる場面はいくつか考えられます。より自然な照明効果を得るために、リムライティングを是非習得していただければと思います。
視線ベクトルと頂点法線
さて、今回のリムライティングですが実装における考え方は意外にも単純です。要はモデルの輪郭部分に照明効果を持たせればいいのですから、普通に考えれば視線ベクトルと法線さえあれば実装できてしまいます。
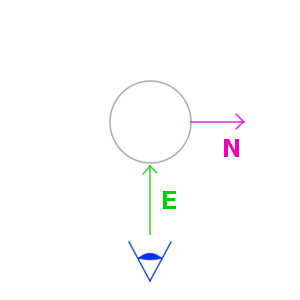
上の図で言うと、視線ベクトル E と法線ベクトル N の角度が直角に近づけば近づくほど、ライティングの係数が大きくなるようにすればいいわけです。これには、視線ベクトルと各頂点の法線との内積を取り、これをクランプした上で 1.0 から減算してやればいいですね。
GLSL でこれを記述すると以下のようになります。
GLSL によるリムライティング係数の計算例
float rim = 1.0 - clamp(dot(normal, eye), 0.0, 1.0);この計算結果を係数として照明効果を施せば、輪郭部分ほど強い照明が掛かるようにすることができます。
ただし、この計算方法ではカメラがどの位置にある場合でも、一律で輪郭部分にリムライトの効果が現れるようになります。冒頭に掲載した男性のシルエット写真を思い出しながら想像してみるとわかると思いますが、現実世界でのリムライティングの効果は、あくまでもモデルの向こう側からバックライトが当たっている場合にだけ現れます。カメラがどの位置にあっても一律でリムライティングの効果が現れてしまうのは不自然です。
そこで、単に視線ベクトルと頂点法線だけでリムライティングの係数を計算するのではなく、視線ベクトルとライトベクトルとを考慮した処理が必要になります。
ライトベクトルを考慮したリムライティング
本来のリムライティングを考えてみると、前述の通り、ライトベクトルを考慮して計算を行なう必要があります。
今回は概念をわかりやすくするために、モデルの位置を原点にレンダリングします。そして、その原点を注視点として眺めるカメラを設定します。さらに、モデルの後方から原点方向に平行光源でライティングします。図式化すると次のような感じですね。
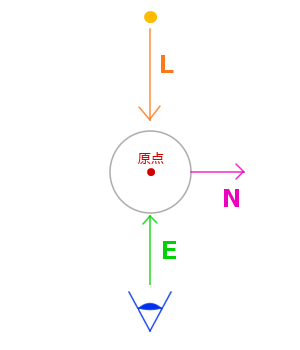
このとき、ライトベクトル L と視線ベクトル E との間で内積を取ることで、二つのベクトルがどの程度向かい合っているかを係数化します。この係数を元に、先ほどのリムライトの掛かり具合を調整してやれば、より自然なリムライティングを行うことが可能になりますね。
それでは、ここまでを踏まえてシェーダのコードを見てみましょう。
リムライティングシェーダ
// 頂点シェーダ
attribute vec3 position;
attribute vec3 normal;
attribute vec4 color;
uniform mat4 mMatrix;
uniform mat4 mvpMatrix;
uniform mat4 invMatrix;
uniform vec3 lightDirection;
uniform vec3 eyes; // カメラの注視点
uniform vec3 eyePosition; // カメラの位置
uniform vec4 rimColor; // リムライトの色
uniform float rimCoef; // リムライトの強さ係数
varying vec4 vColor;
void main(void){
vec3 invLight = normalize(invMatrix * vec4(lightDirection, 0.0)).xyz;
vec3 invEye = normalize(invMatrix * vec4(eyePosition, 0.0)).xyz;
vec3 halfLE = normalize(invLight + invEye);
float diffuse = clamp(dot(normal, invLight), 0.1, 1.0);
float specular = pow(clamp(dot(normal, halfLE), 0.0, 1.0), 50.0);
float rim = pow(1.0 - clamp(dot(normal, invEye), 0.0, 1.0), 5.0);
float dotLE = pow(max(dot(normalize(eyes - eyePosition), normalize(lightDirection)), 0.0), 30.0);
vec4 ambient = rimColor * rimCoef * rim * dotLE;
vColor = color * vec4(vec3(diffuse), 1.0) + vec4(vec3(specular), 1.0) + vec4(ambient.rgb, 1.0);
gl_Position = mvpMatrix * vec4(position, 1.0);
}
// フラグメントシェーダ
precision mediump float;
varying vec4 vColor;
void main(void){
gl_FragColor = vColor;
}ご覧のとおり、今回もほとんどの処理は頂点シェーダ側で行ないます。
頂点シェーダの main 関数の中身は結構な行数がありますが、今回のリムライティング特有の処理はほんの数行だけです。それ以外の部分は、通常のライティングに関するコードで、よくよく見れば今まで何度も登場してきたお馴染みのものです。
さて、それではその問題のリムライティング関連部分を抜粋してみます。
リムライティングの計算を行なっているコード
float rim = pow(1.0 - clamp(dot(normal, invEye), 0.0, 1.0), 5.0);
float dotLE = pow(max(dot(normalize(eyes - eyePosition), normalize(lightDirection)), 0.0), 30.0);ここで登場する変数 rim には、視線ベクトルと頂点法線の内積を用いたリムライティングの係数が入ります。この変数 rim の値が仮に 0 だった場合には、このあと計算する視線ベクトルとライトベクトルの計算がどのような結果になったとしても、リムライトは当たりません。
変数 dotLE には、視線ベクトルとライトベクトルを用いた内積の計算結果が入ります。ライトの向きと視線の向きという二つのベクトルを使って、それぞれがどの程度向かい合っているのかを計算しています。
いずれの係数も、GLSL のビルトイン関数である pow を使ってコントラストを強くしています。これはそもそもリムライトは広範囲に渡る照明効果ではないためです。さらに、頂点シェーダ内ではこれら二つの係数と共に、もう一つ、メインプログラムから uniform 変数としてリムライティングの強さを調整するためのパラメータ rimCoef を受け取るようにしています。この rimCoef はサンプルページの input 要素から値を取得してシェーダに送られてくるようになっていますので、実際に動作するサンプルを見ながら、リムライトがどの程度掛かるのかを調整することが可能です。
メインプログラム側の処理とまとめ
今回のサンプルは、平行光源の向きや視線の向きなど、普段は目に見えないベクトルが大きな役割を果たします。このことを踏まえ、サンプル内では以前解説した線の描画を使っていくつかのベクトルをレンダリングしています。
線のレンダリングによるベクトルの表現

赤い線は X 軸、緑の線が Y 軸です。青い線は Z 軸であると同時に、矢印のような形でライトベクトルの向きを表しています。
上の画像だと、視線の向きと、青い線で表されているライトベクトルがほとんど向き合っていないため、リムライティングの効果は現れていませんね。青い矢印の向かう先にカメラの位置を持ってくると、リムライティングが掛かるようになります。これは実際に動作するサンプルを見てもらったほうが早いでしょう。
メインプログラムとなる javascript のソースでは、この線のレンダリングを行なうための頂点定義やシェーダの定義などが含まれています。ただそれ以外には特別難しいことはしていないので、個別に解説するまでもないと思います。気になる人はソースコードを覗いてみてください。
さて、リムライティング、いかがでしたか。
ベクトルだの内積だのと、いろんな数学用語が出てくるとどうしても話がややこしくなりますね。ただ、落ち着いて考えてみると、案外今まで解説してきたことの応用でしかないということがわかると思います。
リムライティングの実用性を考えてみると、冒頭でも書いたように強い光が当たるシーンなどでは非常に有用な照明効果なのではないかなと思います。より自然なライティング効果を得るための一つの手段として、取り入れてみてはいかがでしょうか。
今回のサンプルも実際に動作するものを見たい場合には以下にリンクがあります。
