視野角を考慮したレイの定義

今回のサンプルの実行結果
3D シーンを自在に操るために
前回は GLSL 内で法線の算出を行い、レイマーチングでライティングされた球体をレンダリングしました。
法線の算出には、ほんの少しだけレイをずらして distance function を呼び出し、そこから勾配を求める方法を用いました。法線は 3D プログラミングにおける非常に重要な要素であり、法線さえ求まってしまえばライティングをはじめとする様々な効果を演出することが可能となります。
少々難しい部分もあるかもしれませんが、今後のためにもぜひ習得しておきましょう。
さて、今回は前回までの内容を踏まえた応用編ということで視野角を考慮したレイの定義について考えてみましょう。これができることによって何がどう役に立つのか、すぐにはイメージしにくいかもしれませんが、順を追ってできる限りわかりやすく解説しますので、がんばってついてきてください。
field of view
当サイトでは、通常の WebGL のプログラムを書く上で補助的な役割をするオリジナルのライブラリとして minMatrix.js を使ってきました。
参考:library: minMatrix.js リファレンス
このオリジナルのライブラリには、行列処理を補助するいくつかのメソッドが含まれていますが、このなかに perspective という名前のメソッドがあります。
このメソッドは、射影座標変換を行うための行列を生成することができるのですが、その引数のなかに fovy という名前の引数があります。この引数には、整数で視野角を渡すことになっています。今回のテーマでもある、視野角。実は既に当サイトでも何度となく登場している概念なんですね。
視野角という言葉から、それがどういったものかはある程度想像がつくのではないかと思います。要は、スクリーンに映し出す世界をどのくらいの広さで切り取るのか、これをコントロールするために必要となる概念です。英語だと視野角は[ field of view ]となります。この頭文字を取って[ fov ]というように略して表記されることもあります。
視野角は何度も言うとおり、見える領域を正確にコントロールする上で重要な概念です。前回までに紹介してきたレイの算出方法は視野角の概念を用いていません。ただ、これまでの方法でも実用上で問題があるわけではないのです。
視野角を用いたレイの算出ができることによって、スクリーンに映し出す三次元空間の領域を自由に制御できるようになります。カメラワークの都合上、そのほうが勝手がいい場合もあるでしょう。概念を理解しておいて損をすることはないはずです。
視野角の概念を取り入れたレイの定義
ここからはちょっとだけ数学寄りの話になります。視野角の概念を理解するうえでどうしても避けて通れません。しかし、心配は要りません。割と、簡単です。
まず、さっくりとコードから見てみましょう。
視野角によるレイの定義
const float PI = 3.14159265;
const float angle = 60.0;
const float fov = angle * 0.5 * PI / 180.0;
void main(void){
// fragment position
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, resolution.y);
// ray
vec3 ray = normalize(vec3(sin(fov) * p.x, sin(fov) * p.y, -cos(fov)));
// 以下続くまず最初に定数をいくつか定義しています。円周率を表す PI と、視野角を表す angle があり、それを用いて変数 fov に何かしらの値を代入しています。
よく見てみてください。
なんのことはありません。ここは、視野角に指定された度数のちょうど半分の度数でラジアンを算出しているだけです。 angle に 0.5 を掛けていることからもわかりますね。
そして、ここで求められた値を使ってレイを定義しているのがわかると思います。
レイの定義部分を抜粋
vec3 ray = normalize(vec3(sin(fov) * p.x, sin(fov) * p.y, -cos(fov)));まず X と Y については sin を使っています。Z は cos ですね。このような計算でレイが定義できる仕組みは、三角関数を理解していればおのずとわかると思います。
三角関数がわからないという人には、勉強しろ! と一蹴してもいいのですが、3D の数学にあまり馴染みのない人もいるかもしれませんので、もう少しだけ踏み込んでみましょう。
これらの概念を理解するうえでは、いわゆる三平方の定理を持ち出しつつ考えていくとイメージしやすいかなと思います。三平方の定理はピタゴラスの定理とも呼ばれていますね。これはたぶん、中学校あたりで習う数学だったような気がします。
30°を含む直角三角形
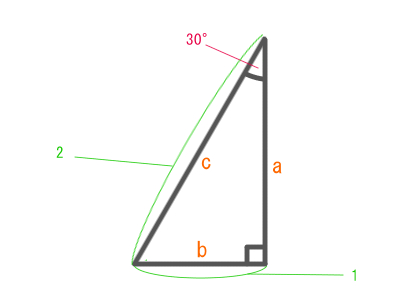
三平方の定理で考えると、直角と 30°、そして 60°からなる三角形の場合、上の図で示したように辺の長さの比が 1 対 2 対 ルート 3 となります。この図式を覚えておいてください。
そして、今回は話をわかりやすくするために、次のような状況を想定します。
- カメラは
(0.0, 0.0, 2.0)の位置に置く - レンダリングする球体を原点を中心にして置く
- 球体の半径は 1.0 とする
- 視野角は度数表記で 60°とする
はい、ここまでを踏まえて、次の図を見てみましょう。
視野角の概念図
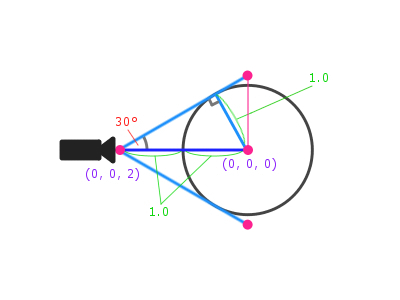
先ほど示した状況をそのまま図解しました。
視野角が 60 度だとすると、上の図のように 30°の角をカメラ側に、直角三角形が上下に展開している状態だと考えることができますね。そして、先ほどの三平方の定理の図解で見たように、緑色の文字で辺の長さが書かれている部分についても破たんなく正しい解になっていることが見てわかると思います。
注目すべきはピンクの点です。
上のほうにある点と原点にある点、これを結ぶピンク色の線が引かれていますね。このピンク色の線の長さは sinθ で求めることができます。これが要は三角関数の基礎です。ここまでわかれば、レイの定義で X と Y の計算に sin を用いた意味がわかるでしょう。
同様に、上の図で濃い青で引かれている線。この長さは cosθで求まります。ですから、レイの定義のところでは Z の値を求めるのに cos が使われていたわけです。
実際にレンダリング結果を見てみる
さて、ちょっと小難しい数学の話が続きましたが、視野角によるレイの定義をする場合には、視野角のちょうど半分の度数をラジアンに変換してやり、そこからサインとコサインを割り出してやればいいわけです。
実際に、フラグメントシェーダの全コードを見てみましょう。
フラグメントシェーダのコード
precision mediump float;
uniform float time;
uniform vec2 mouse;
uniform vec2 resolution;
const float PI = 3.14159265;
const float angle = 60.0;
const float fov = angle * 0.5 * PI / 180.0;
vec3 cPos = vec3(0.0, 0.0, 2.0);
const float sphereSize = 1.0;
const vec3 lightDir = vec3(-0.577, 0.577, 0.577);
float distanceFunc(vec3 p){
return length(p) - sphereSize;
}
vec3 getNormal(vec3 p){
float d = 0.0001;
return normalize(vec3(
distanceFunc(p + vec3( d, 0.0, 0.0)) - distanceFunc(p + vec3( -d, 0.0, 0.0)),
distanceFunc(p + vec3(0.0, d, 0.0)) - distanceFunc(p + vec3(0.0, -d, 0.0)),
distanceFunc(p + vec3(0.0, 0.0, d)) - distanceFunc(p + vec3(0.0, 0.0, -d))
));
}
void main(void){
// fragment position
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, resolution.y);
// ray
vec3 ray = normalize(vec3(sin(fov) * p.x, sin(fov) * p.y, -cos(fov)));
// marching loop
float distance = 0.0;
float rLen = 0.0;
vec3 rPos = cPos;
for(int i = 0; i < 16; i++){
distance = distanceFunc(rPos);
rLen += distance;
rPos = cPos + ray * rLen;
}
// hit check
if(abs(distance) < 0.001){
vec3 normal = getNormal(rPos);
float diff = clamp(dot(lightDir, normal), 0.1, 1.0);
gl_FragColor = vec4(vec3(diff), 1.0);
}else{
gl_FragColor = vec4(vec3(0.0), 1.0);
}
}前回のサンプルを、そのままレイの定義方法だけ変えたコードです。
マーチングループや法線の算出については前回と全く同じものになります。これを実行してみると、先ほどの図を思い出してもらえればわかると思いますが、球体の上下にほんの少しだけ隙間がある状態で、ほぼスクリーンいっぱいの球体がレンダリングされるはずです。
今回のサンプルを実際に動作させてみれば、正しくレイが定義できていることがわかると思います。
まとめ
さて、ほとんどが数学的な話でしたので面白味はあまりなかったと思いますが、視野角の概念でレイを定義する方法、理解できたでしょうか。
視野角によるレイの定義ができると、レンダリングする領域の範囲を制御しやすくなります。この機会にその概念を正しく理解しておきましょう。
ただ、正直なところ、この程度の内容でテキスト一回分使ってよかったのかなあという気もします。ふたを開けてみれば、要は、三角関数をただ使っているだけですからね。しかし、コードだけを見てなんとなく意味を理解したつもりになっているよりも、図解してみたり、細部まで理屈を考えてみたりしながら理解したほうが、今後の様々な場面で役に立つ可能性があると思ったので、今回のテキストを書きました。
レイマーチングに限らず、レイトレーシングの分野では極力コードを短く記述することが多いです。当サイトでは、できる限り省略せずに、簡単なことから詳細に解説するように心がけていきたいと思っています。もし、わからないことがあったら気軽に twitter などで質問してください。説明できることであれば、解説します。
実際に動作するサンプルはいつものように以下のリンクから。
