再帰処理と移動・回転・拡大縮小
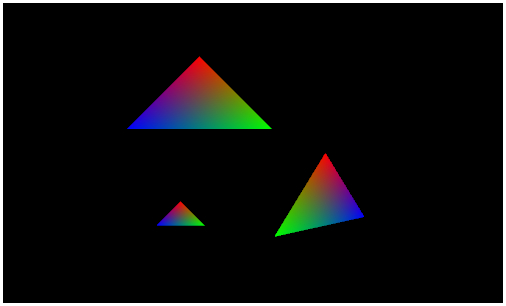
今回のサンプルの実行結果
モデル座標変換行列の妙
前回はモデル座標変換行列を操作して複数モデルのレンダリングを行ないました。今回は、その延長上の処理として、複数のモデルに、異なるモデル座標変換を適用して移動や回転、拡大縮小を行なってみたいと思います。
前回のテキストを読んだ方ならわかると思いますが、3D レンダリングの世界では、VBO や一部の座標変換行列を使いまわすことによって、少ないリソースで大量のモデルを描画することが可能です。当然、計算の負荷も少なくなるので高速に動作させることができ一石二鳥ですね。
逆に言うと、モデル座標変換を上手に使いこなすことで、効率良くレンダリングを行なうことが可能であり、これこそがモデル座標変換の妙味でもあるわけです。
今回は、合計三つのポリゴンを描画してみます。一つは円を描くように移動するポリゴン、一つは Y 軸を中心に回転するポリゴンです。三つ目のポリゴンは、拡大縮小を行なってからレンダリングを行なってみます。
恒常ループ処理を実装する
前回までのサンプルでは、canvas 上の描画を更新するのは一回だけでした。今回のサンプルでは、変化の過程を常に更新し続け、いわゆるアニメーションを行なうようにソースを修正します。
アニメーション処理を行なうためには、常に画面を更新するための恒常ループを実装する必要があります。javascript による恒常ループにはいろいろな方法が考えられますが、当サイトでは基本的に setTimeout メソッドを使うことにします。
ここで登場した setTimeout は javascript に於ける window オブジェクトの組み込みメソッドで、指定された時間が経過した後、指定された処理を実行する機能があります。経過時間はミリ秒単位で指定しますので、たとえば 1 秒は 1000 ミリ秒という具合に、秒数を千倍して指定します。
setTimeout を用いた再帰処理
先述のとおり、 setTimeout メソッドを使うことで繰り返しループ処理を行うことが可能なわけですが、具体的にはどうすればいいのでしょうか。
setTimeout メソッドは、第一引数に呼び出すことになる関数(処理)を、第二引数に関数を呼び出す経過時間をミリ秒で指定します。この第一引数に、今現在実行されている処理そのものを指定することができれば、その処理が恒常的に呼ばれ続けることになりますね。
- 関数 A が実行される
- 関数 A の中で setTimeout に関数 A をセット
- 指定時間経過後に関数 A が呼び出される
このような流れで、WebGL の描画を行なう部分を丸々詰め込んだ関数を作成して、再帰的に呼び出し続けるようにします。
arguments クラスと callee プロパティ
関数が、その関数自身を呼び出す仕組みは、関数に名前が付いていれば簡単に実装できます。関数の中で、その関数の名前を書いて普通に呼び出せばいいだけだからです。しかし、関数自体が名前を持っていない場合には呼び出す方法が一見無いように思えます。
しかしこれには解決法があって、 arguments クラスの callee プロパティを参照することで、関数自身への参照を得ることが可能です。 arguments クラスは関数が呼び出された瞬間に自動的に生成されます。そして callee プロパティを参照することでその関数自身への参照を得ることができます。この手法を用いれば、仮に関数が名前を持たない無名関数であったとしても再帰呼び出しが可能です。
今回のテキストでの再帰処理は、ここで説明したような setTimeout + arguments.callee の合わせ技で実現してみることにしましょう。
再帰関数の中に詰め込む処理を選別
再帰呼び出しされる関数の中には、必要最低限のものだけを詰め込みます。繰り返し呼び出される処理の中に、余分な処理を詰め込んでしまうと無駄に処理が重たくなってしまうからですね。
たとえば、WebGL コンテキストの取得や、VBO やシェーダの生成などは、毎回呼び出す必要はありませんね。一度生成されたオブジェクトを再利用すればいいだけだからです。同様の理由で、ビュー座標変換行列とプロジェクション座標変換行列を生成する部分も再帰処理に含める必要はありませんね。毎回同じものを使うだけだからです。
そうなると、再帰処理の中に含める処理はかなり限定されることがわかります。具体的には以下のものだけを再帰処理に組み込みます。
- 画面のクリア(初期化)
- モデル座標変換行列の生成
- uniform への座標変換行列の登録
- 描画命令
- 画面の更新
- setTimeout + arguments.callee
さて、このことを踏まえ、再帰処理周辺のコードを抜粋して見てみましょう。
再帰処理周辺のコードを抜粋
// minMatrix.js を用いた行列関連処理
// matIVオブジェクトを生成
var m = new matIV();
// 各種行列の生成と初期化
var mMatrix = m.identity(m.create());
var vMatrix = m.identity(m.create());
var pMatrix = m.identity(m.create());
var tmpMatrix = m.identity(m.create());
var mvpMatrix = m.identity(m.create());
// ビュー×プロジェクション座標変換行列
m.lookAt([0.0, 0.0, 5.0], [0, 0, 0], [0, 1, 0], vMatrix);
m.perspective(45, c.width / c.height, 0.1, 100, pMatrix);
m.multiply(pMatrix, vMatrix, tmpMatrix);
// カウンタの宣言
var count = 0;
// 恒常ループ
(function(){
// canvasを初期化
gl.clearColor(0.0, 0.0, 0.0, 1.0);
gl.clearDepth(1.0);
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
// カウンタをインクリメントする
count++;
// カウンタを元にラジアンを算出
var rad = (count % 360) * Math.PI / 180;
// モデル1は円の軌道を描き移動する
var x = Math.cos(rad);
var y = Math.sin(rad);
m.identity(mMatrix);
m.translate(mMatrix, [x, y + 1.0, 0.0], mMatrix);
// モデル1の座標変換行列を完成させレンダリングする
m.multiply(tmpMatrix, mMatrix, mvpMatrix);
gl.uniformMatrix4fv(uniLocation, false, mvpMatrix);
gl.drawArrays(gl.TRIANGLES, 0, 3);
// モデル2はY軸を中心に回転する
m.identity(mMatrix);
m.translate(mMatrix, [1.0, -1.0, 0.0], mMatrix);
m.rotate(mMatrix, rad, [0, 1, 0], mMatrix);
// モデル2の座標変換行列を完成させレンダリングする
m.multiply(tmpMatrix, mMatrix, mvpMatrix);
gl.uniformMatrix4fv(uniLocation, false, mvpMatrix);
gl.drawArrays(gl.TRIANGLES, 0, 3);
// モデル3は拡大縮小する
var s = Math.sin(rad) + 1.0;
m.identity(mMatrix);
m.translate(mMatrix, [-1.0, -1.0, 0.0], mMatrix);
m.scale(mMatrix, [s, s, 0.0], mMatrix)
// モデル3の座標変換行列を完成させレンダリングする
m.multiply(tmpMatrix, mMatrix, mvpMatrix);
gl.uniformMatrix4fv(uniLocation, false, mvpMatrix);
gl.drawArrays(gl.TRIANGLES, 0, 3);
// コンテキストの再描画
gl.flush();
// ループのために再帰呼び出し
setTimeout(arguments.callee, 1000 / 30);
})();ソースコードの全文は、最後にリンクを貼ってあるサンプルのページから辿っていけば見ることができます。また、HTML やシェーダのソースに修正箇所はありません。
今回の処理でポイントとなるのは、無名関数の外側で宣言している変数 count の使い方です。無名関数の中では、毎回この変数をインクリメントするようにしていますね。そして、この変数 count の値を使ってモデル座標変換を行なっています。
変数 count を 360 で割り、その余りを使ってラジアンを計算します。それを行っているのが下記のコードですね。
ラジアンを取得している部分
var rad = (count % 360) * Math.PI / 180;変数 count がどれほど大きな数になっても、割った余りを用いれば必ずその範囲は 0 ~ 359 のなかに収まります。そこにラジアンを求める公式を当てることで、変数 rad には正確なラジアンを取得できるわけですね。そして、ここで得られたラジアンを一つのパラメータとして、モデル座標変換を行なっていきます。
一つ目のモデルは、ラジアンからサインとコサインを求め X と Y の移動成分としてそれぞれ与えています。
二つ目のモデルは、Y 軸を中心とした回転を行なうためにラジアンを使っていますね。
三つ目のモデルは拡大縮小するためのスケーリング値にラジアンから求めたサインの値を使っています。
ここで頻繁に登場している各種座標変換のためのメソッド(multiplyやrotateなど)は、minMatrix.js に実装されているものですので注意しましょう。引数の指定の仕方などは以前のテキスト(minMatrix.js と座標変換行列)で詳しく解説していますので参考にしてみてください。
また、モデル座標変換の順序にも気をつけましょう。移動や回転、拡大縮小などの座標変換は、それを行なう順序を間違えると結果がまるで変わってしまいます。これも、先ほどリンクを貼った以前のテキスト内で詳しく説明していますので、曖昧な人はしっかり復習しておくことをオススメします。
まとめ
今回は恒常ループを実現するための再帰処理について、そしてモデル座標変換行列の処理について解説しました。今後は、動きのあるサンプルを用いることが多くなってくると思いますので、今回紹介したような恒常ループを使う場面が増えていくはずです。
無名関数や、関数の再帰呼び出しなどは少し難しい概念かもしれませんが、落ち着いて考えればわかると思いますので焦らず理解していっていただければと思います。要望が多いようなら、そういった部分に関しては個別にテキストを用意するべきなのかなとも思いますが。
さて次回ですが、インデックスバッファについてやろうと思います。
今回のサンプルは以下のリンクから実際に動作させることが可能ですので、是非参考にしてみてください。
